Question

【题目】如图1，在□ABCD中，AE⊥BC于E，E恰为BC的中点，tanB=2。

（1）求证：AD=AE；

（2）如图2，点P在BE上，作EF⊥DP于点F，连结AF，求证：DF-EF=AF；

（3）请你在图3中画图探究：当P为射线EC上任意一点（P不与点E重合）时，作EF⊥DP于点F，连结AF，线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论为____________。

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）画图见解析，

①当EP在线段BC上时,有DFEF=AF

②当EP2BC时,DF+EF=AF.

【解析】试题分析：（1）首先根据∠B的正切值知：AE=2BE，而E是BC的中点，结合平行四边形的对边相等即可得证．

（2）此题要通过构造全等三角形来求解；作GA⊥AF，交BD于G，通过证△AFE≌△AGD，来得到△AFG是等腰直角三角形且EF=GD，由此得证．

（3）辅助线作法和解法同（2），只不过结论有所不同而已．

试题解析：

（1）在Rt△ABE中，∠AEB=90°，

∴tanB==2，

∴AE=2BE。

∵E为BC的中点，

∴BC=2BE，

∴AE=BC。

∵ABCD是平行四边形，

∴AD=BC，

∴AE=AD。

（2）在DP上截取DH=EF（如图）

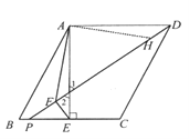
∵四边形ABCD是平行四边形，AE⊥BC，

∴∠EAD=90°。

∵EF⊥PD，∠l=∠2，

∴∠ADH=∠AEF。

∵AD=AE，

∴△ADH≌△AEF，

∴∠HAD=∠FAE，AH=AF，

∴∠FAH=90°。

在Rt△FAH中，AH=AF，

∴FH=AF，

∴FH=FD-HD=FD-EF=AF。

即DF-EF=AF。

（3）按题目要求所画图形见图，

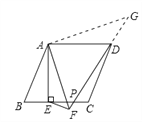
①当EP在线段BC上时,有DFEF=AF

②当EP2BC时,DF+EF=AF.

③当EP>2BC时,EFDF=AF.

点睛:此题主要考查的是平行四边形的性质以及全等三角形的判定和性质,难度适中,正确的构造出全等三角形是解答此题的关键.