题目内容
【题目】在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上。
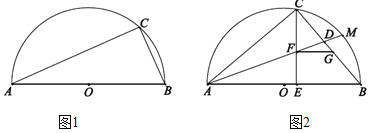
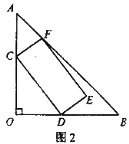
(1)如图1,若C、D恰好是边AO、OB的中点,则此时矩形CDEF的面积为_________;
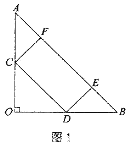
(2)如图2,若![]() =
=![]() ,求矩形CDEF面积的最大值。
,求矩形CDEF面积的最大值。
【答案】(1)S矩形CDEF=16;
(2)矩形CDEF面积的最大值为![]() 。
。
【解析】试题分析:(1)因为当C、D是边AO,OB的中点时,点E、F都在边AB上,且CF⊥AB,所以可求出CD的值,进而求出CF的值,矩形CDEF的面积可求出;
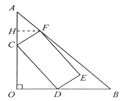
(2)设CD=x,CF=y.过F作FH⊥AO于H.在 Rt△COD中,用含x和y的代数式分别表示出CO、AH的长,进而表示出矩形CDEF的面积,再配方可求出面积的最大值.
试题解析:
(1)如图,当C、D是边AO,OB的中点时,
点E、F都在边AB上,且CF⊥AB。
∵OA=OB=8,
∴OC=AC=OD=4。
∵∠AOB=90°,
∴CD=4![]() 。
。
在Rt△ACF中,
∵∠A=45°,
∴CF=2![]() ,
,
∴S矩形CDEF=4![]() ×2
×2![]() =16。
=16。
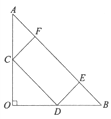
(2)设CD=x,CF=y。过F作FH⊥AO于H。在Rt△COD中,
∵tan∠CDO=![]() ,
,
∴sin∠CDO=![]() ,cos∠CDO=
,cos∠CDO=![]() ,
,
∴CO=![]() x
x
∵∠FCH+∠OCD=90°,
∴∠FCH+∠CDO,
∴HC=y·cos∠FCH=![]() y,
y,
∴FH=![]() y。
y。
∵△AHF是等腰直角三角形,
∴AH=FH=![]() y,
y,
∴AO=AH+HC+CO。
∴![]() ,
,
∴y=![]() (40-4x)
(40-4x)
易知S矩形CDEF=xy=![]()
![]() [(x-5)2-25],
[(x-5)2-25],
∴当x=5时,矩形CDEF面积的最大值为![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目