��Ŀ����
����Ŀ����ͼ1��ʾ����֪��ABC�У���BAC=90�㣬AB=AC��AE�ǹ���A��һ��ֱ�ߣ���B���C����AE����࣬BD��AE��D�㣬CE��AE��E�㣮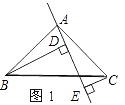
��1����֤��BD=DE+CE
��2����ֱ��AE�Ƶ�A��ת��ͼ2��ʾ��λ��ʱ��BD��CE�������������䣬��BD ��DE��CE�Ĺ�ϵ��Σ�������֤����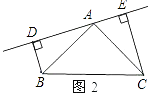
��3����ֱ��AE�Ƶ�A��ת��ͼ3��ʾ��λ��ʱ��BD��CE�������������䣬��BD ��DE��CE�Ĺ�ϵ��Σ�ֱ��д�����������֤����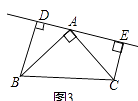
���𰸡�
��1��
֤������BD��AE��D��CE��AE��E��
���ADB=��AEC=90�㣮
�ߡ�BAC=90�㣬��ADB=90�㣬
�ߡ�ABD+��BAD=��CAE+��BAD=90�㣬
���ABD=��CAE
�ڡ�ABD �͡�CAE�У�
��ABD=��CAE����ADB=��CEA��AB=AC
���ABD�ա�CAE��AAS��
��BD=AE��AD=CE
��AE=AD+DE��
��BD=DE+CE
��2��
�⣺BD=DE��CE
֤�����£�
��BD��AE��D��CE��AE��E��
���DAB+��DBA=90��
�ߡ�BAC=90�㣬
���DAB+��CAE=90�㣬
���DBA=��CAE��
�ڡ�DBA�͡�EAC�У�
��D=��E=90�㣬��DBA=��CAE��AB=AC
��DBA�ա�EAC��AAS��
��BD=AE��AD=CE
BD=AE=DE��AD=DE��CE
��3��
�⣺��BD��AE��D��CE��AE��E��
���DAB+��DBA=90��
�ߡ�BAC=90�㣬
���DAB+��CAE=90�㣬
���DBA=��CAE��
�ڡ�DBA�͡�EAC�У�
��D=��E=90�㣬��DBA=��CAE��AB=AC
��DBA�ա�EAC��AAS��
��BD=AE��AD=CE
�֡�ED=AD+AE��
��DE=BD+CE��
����������1��������֪������֤�á�BAD=��ACE���Ҹ���ȫ�������ε��ж���֤����ABD�ա�CAE�����ݸ��߶εĹ�ϵ���ɵý��ۣ���2��BD=DE+CE������ȫ�������ε��ж���֤����ABD�ա�CAE�����ݸ��߶εĹ�ϵ���ɵý��ۣ���3��ͬ������BD=DE+CE�Գ�����