题目内容
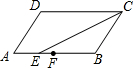
如图,P为平行四边形ABCD内一点,过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点,若SAHPE=3,SPFCG=5,则S△PBD=______.


显然EPGD、GPFC、EPHA、PHBF均为平行四边形,
∴S△DEP=S△DGP=
S平行四边形DEPG,
∴S△PHB=S△PBF=
S平行四边形PHBF,
又S△ADB=S△EPD+S平行四边形AHPE+S△PHB+S△PDB①
S△BCD=S△PDG+S平行四边形PFCG+S△PFB-S△PDB②
①-②得0=S平行四边形AHPE-S平行四边形PFCG+2S△PDB,
即2S△PBD=5-3=2
∴S△PBD=1.
故答案为:1.
∴S△DEP=S△DGP=
| 1 |
| 2 |
∴S△PHB=S△PBF=
| 1 |
| 2 |
又S△ADB=S△EPD+S平行四边形AHPE+S△PHB+S△PDB①
S△BCD=S△PDG+S平行四边形PFCG+S△PFB-S△PDB②
①-②得0=S平行四边形AHPE-S平行四边形PFCG+2S△PDB,
即2S△PBD=5-3=2
∴S△PBD=1.
故答案为:1.

练习册系列答案
相关题目