题目内容
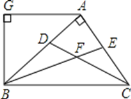
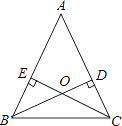
【题目】如图,已知△ABC和△ADE均为等边三角形,点O是AC的中点,点D在射线BO上,连结OE,EC,则∠ACE=_____°;若AB=1,则OE的最小值=_____.

【答案】30 ![]()
【解析】
根据等边三角形的性质可得OC=![]() AC,∠ABD=30°,根据"SAS"可证△ABD≌△ACE,可得∠ACE=30°=∠ABD,当OE⊥EC时,OE的长度最小,根据直角三角形的性质可求OE的最小值.
AC,∠ABD=30°,根据"SAS"可证△ABD≌△ACE,可得∠ACE=30°=∠ABD,当OE⊥EC时,OE的长度最小,根据直角三角形的性质可求OE的最小值.
解:∵△ABC的等边三角形,点O是AC的中点,
∴OC=![]() AC,∠ABD=30°
AC,∠ABD=30°
∵△ABC和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△ABD≌△ACE(SAS)
∴∠ACE=30°=∠ABD
当OE⊥EC时,OE的长度最小,
∵∠OEC=90°,∠ACE=30°
∴OE最小值=![]() OC=
OC=![]() AB=
AB=![]()
故答案为:30,![]()

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目