题目内容
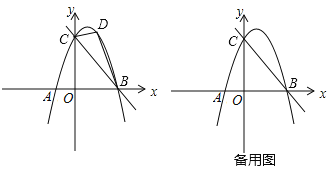
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数![]() 的图象交于第二、四象限内的A,B两点,与
的图象交于第二、四象限内的A,B两点,与![]() 轴交于C点,过点A作AH⊥
轴交于C点,过点A作AH⊥![]() 轴,垂足为H,OH=3,tan∠AOH=
轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(
,点B的坐标为(![]() ,﹣2).
,﹣2).
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积.

【答案】(1)反比例函数解析式为y=-![]() .一次函数的解析式为y=-x+1.(2)
.一次函数的解析式为y=-x+1.(2)![]() .
.
【解析】
(1)由OH和tan∠AOH的值即可求出点A的坐标,利用反比例函数图象上点的坐标特征即可求出k值和点B的坐标,再根据点A、B的坐标利用待定系数法即可求出直线AB的解析式; (2)将x=0代入直线AB的解析式中求出y值,由此即可得出OC的长度,再根据三角形的面积公式即可求出△AOC的面积.
(1)∵OH=3,tan∠AOH=![]() ,
,
∴AH=OHtan∠AOH=2,
∴点A的坐标为(-2,3).
∵点A在反比例函数y=![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=-2×3=-6,
∴反比例函数解析式为y=-![]() .
.
∵点B(m,-2)在反比例函数y=-![]() 的图象上,
的图象上,
∴m=3,
∴点B的坐标为(3,-2).
将A(-2,3)、B(3,-2)代入y=ax+b,![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为y=-x+1.
(2)当x=0时,y=-x+1=1,
∴点C的坐标为(0,1),
∴OC=1,
∴S△AOB=S△AOC+S△BOC=![]() ×1×2+
×1×2+![]() ×1×3=
×1×3=![]() .
.

【题目】把弹簧的上端固定,在其下端挂物体,下表是测得的弹簧长度![]() 与所挂物体的质量
与所挂物体的质量![]() 的一组对应值:
的一组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 15 | 15.5 | 16 | 16.5 | 17 | 17.5 | … |
(1)表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)弹簧的原长是_______![]() ,物体每增加
,物体每增加![]() ,弹簧的长度增加_________
,弹簧的长度增加_________![]() .
.
(3)请你估测一下当所挂物体为![]() 时,弹簧的长度是______
时,弹簧的长度是______![]() .
.