Question

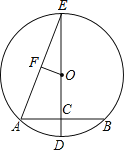
【题目】如图，在⊙O中，DE是⊙O的直径，AB是⊙O的弦，AB的中点C在直径DE上．已知AB=8cm，CD=2cm

（1）求⊙O的面积；

（2）连接AE，过圆心O向AE作垂线，垂足为F，求OF的长．

Answer 1

【答案】（1）S=25π；（2）OF=.

【解析】

（1）连接OA，根据AB=8cm，CD=2cm，C为AB的中点，设半径为r，由勾股定理列式即可求出r，进而求出面积．

（2）在Rt△ACE中，已知AC、EC的长度，可求得AE的长，根据垂径定理可知：OF⊥AE，FE=FA，利用勾股定理求出OF的长．

解：（1）连接OA，如图1所示

∵C为AB的中点，AB=8cm，

∴AC=4cm

又∵CD=2cm

设⊙O的半径为r，则（r-2）2+42=r2

解得：r=5

∴S=πr2=π×25=25π

（2）OC=OD-CD=5-2=3

EC=EO+OC=5+3=8

∴EA===4

∴EF===2

∴OF===