题目内容
【题目】如图，直线AB过点A（3,0），B（0,2）
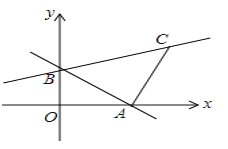
（1）求直线AB的解析式。
（2）过点A作AC⊥AB且AC∶AB=3∶4，求过B、C两点直线的解析式．
【答案】（1）
（2）
【解析】
（1）用待定系数法直接代入A，B的坐标即可；
（2）过C点作CD⊥x轴于D点，用三角形的相似求出C点的坐标，再用待定系数法求过B、C两点直线的解析式即可.
（1）设直线AB的解析式为：
代入A（3,0），B（0,2）得：
解得：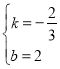
∴直线AB的解析式为
（2）如图：过C点作CD⊥x轴于D点，
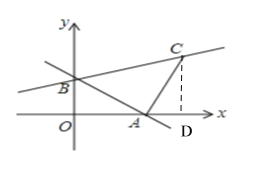
∵AC⊥AB
∴∠CAD+∠OAB=90°，∠OAB+∠OBA=90°
∴∠CAD=∠OBA
又∠BOA=∠ADC=90°
∴△AOB∽CDA
∴
∵AC∶AB=3∶4
∴
∴
所以C点的坐标为
设直线BC的解析式为：
代入B（0,2），C 得：
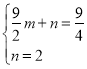
解得：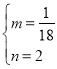
∴过B、C两点直线的解析式为：
练习册系列答案
相关题目
