题目内容
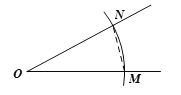
【题目】如图,在Rt△AOB中,∠AOB=90°,已知点A(﹣1,﹣1),点B在第二象限,OB=![]() ,抛物线
,抛物线![]() 经过点A和B.
经过点A和B.
(1)求点B的坐标;
(2)求抛物线![]() 的对称轴;
的对称轴;
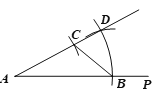
(3)如果该抛物线的对称轴分别和边AO、BO的延长线交于点C、D,设点E在直线AB上,当△BOE和△BCD相似时,直接写出点E的坐标.

【答案】(1)B(﹣2,2);(2)对称轴是x=1;(3)E的坐标(﹣![]() ,0),(﹣
,0),(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题(1)、根据互相垂直的两直线一次项系数的乘积为-1,可得BO的解析式,根据勾股定理可得B点坐标;(2)、根据待定系数法可得函数解析式,根据配方法可得答案;(3)、根据待定系数可得AB的解析式,根据自变量与函数值的对应关系可得E、F点的坐标,分类讨论:△BCD∽△BEO时可得F点坐标;△BCD∽△BOE时根据相似于同一个三角形的两个三角形相似可得△BFO∽△BOE,根据相似三角形的性质可得BF的长,根据勾股定理可得F点坐标.
试题解析:(1)、AO的解析式为y=x,AO⊥BO,则BO的解析式为y=-x,
设B点坐标为(a,-a),由![]() 得:a=2(不符合题意,舍去),或a=-2
得:a=2(不符合题意,舍去),或a=-2
故点B的坐标为(-2,2);
(2)、将A、B点坐标代入函数解析式得: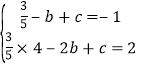 ,解得:
,解得: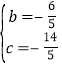 ,
,
∴函数解析式为:![]() ,
,
∴函数的对称轴是:直线x=1;
(3)、点E的坐标为:(﹣![]() ,0),(﹣
,0),(﹣![]() ,﹣
,﹣![]() ).
).

练习册系列答案
相关题目