题目内容
【题目】如图,AB为圆O的直径,点C为圆O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与圆O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,圆O的半径为3,并且∠CAB=30°,求AD的长.

【答案】(1)CD与圆O的位置关系是相切,理由详见解析;(2) AD=![]() .
.
【解析】
(1)连接OC,求出OC和AD平行,求出OC⊥CD,根据切线的判定得出即可;
(2)连接BC,解直角三角形求出BC和AC,求出△BCA∽△CDA,得出比例式,代入求出即可.
(1)CD与圆O的位置关系是相切,
理由是:连接OC,
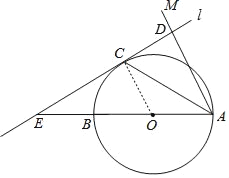
∵OA=OC,
∴∠OCA=∠CAB,
∵∠CAB=∠CAD,
∴∠OCA=∠CAD,
∴OC∥AD,
∵CD⊥AD,
∴OC⊥CD,
∵OC为半径,
∴CD与圆O的位置关系是相切;
(2)连接BC,
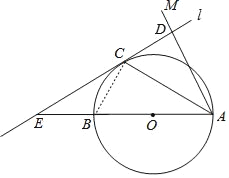
∵AB是⊙O的直径,
∴∠BCA=90°,
∵圆O的半径为3,
∴AB=6,
∵∠CAB=30°,
∴![]()
∵∠BCA=∠CDA=90°,∠CAB=∠CAD,
∴△CAB∽△DAC,
∴![]()
∴![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目