Question

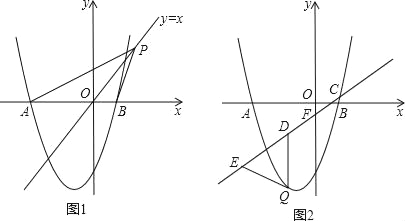
【题目】如图，抛物线y=ax2+2x﹣3与x轴交于A、B两点，且B（1，0）

（1）求抛物线的解析式和点A的坐标；

（2）如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；

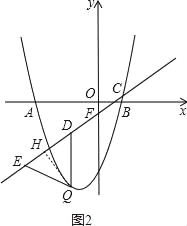
（3）如图2，已知直线y=x﹣分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

Answer 1

【答案】（1）A点坐标为（﹣3，0）；（2）；P点坐标为（， ）；（3）以QD为腰的等腰三角形的面积最大值为．

【解析】试题分析：（1）把B点的坐标代入抛物线的解析式，求出a的值即可，令y=0，解方程求得x的值，即可得点A的坐标；（2）当点P在x轴上方时，连接AP交y轴于点B′，可证△OBP≌△OB′P，可求得B′坐标，利用待定系数法可求得直线AP的解析式，联立直线y=x，可求得P点坐标；当点P在x轴下方时，同理可求得∠BPO=∠B′PO，又∠B′PO在∠APO的内部，可知此时没有满足条件的点P；（3）过Q作QH⊥DE于点H，由直线CF的解析式可求得点C、F的坐标，结合条件可求得tan∠QDH，可分别用DQ表示出QH和DH的长，分DQ=DE和DQ=QE两种情况，分别用DQ的长表示出△QDE的面积，再设出点Q的坐标，利用二次函数的性质可求得△QDE的面积的最大值．

试题解析：

（1）把B（1，0）代入y=ax2+2x﹣3，

可得a+2﹣3=0，解得a=1，

∴抛物线解析式为y=x2+2x﹣3，

令y=0，可得x2+2x﹣3=0，解得x=1或x=﹣3，

∴A点坐标为（﹣3，0）；

（2）若y=x平分∠APB，则∠APO=∠BPO，

如图1，若P点在x轴上方，PA与y轴交于点B′，

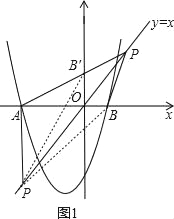
由于点P在直线y=x上，可知∠POB=∠POB′=45°，

在△BPO和△B′PO中，

∠POB=∠PCB/，OP=OP，∠BPO=∠B/PO，

∴△BPO≌△B′PO（ASA），

∴BO=B′O=1，

设直线AP解析式为y=kx+b，把A、B′两点坐标代入可得

，解得，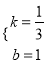

∴直线AP解析式为y=x+1，

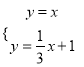联立，解得，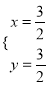

∴P点坐标为（， ）；

若P点在x轴下方时，同理可得△BOP≌△B′OP，

∴∠BPO=∠B′PO，

又∠B′PO在∠APO的内部，

∴∠APO≠∠BPO，即此时没有满足条件的P点，

综上可知P点坐标为（， ）；

（3）如图2，作QH⊥CF，交CF于点H，

∵CF为y=x﹣，

∴可求得C（，0），F（0，﹣），

∴tan∠OFC==，

∵DQ∥y轴，

∴∠QDH=∠MFD=∠OFC，

∴tan∠HDQ=，

不妨设DQ=t，DH=t，HQ=t，

∵△QDE是以DQ为腰的等腰三角形，

∴若DQ=DE，则S△DEQ=DEHQ=×t×t=t2，

若DQ=QE，则S△DEQ=DEHQ=×2DHHQ=×t×t=t2，

∵t2＜t2，

∴当DQ=QE时△DEQ的面积比DQ=DE时大．

设Q点坐标为（x，x2+2x﹣3），则D（x， x﹣），

∵Q点在直线CF的下方，

∴DQ=t=x﹣﹣（x2+2x﹣3）=﹣x2﹣x+，

当x=﹣时，tmax=3，

∴（S△DEQ）max=t2=，

即以QD为腰的等腰三角形的面积最大值为．