题目内容
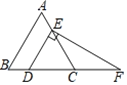
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4,点D是AB的中点,动点P、Q同时从点D出发(点P、Q不与点D重合),点P沿D→A以1cm/s的速度向中点A运动.点Q沿D→B→D以2cm/s的速度运动.回到点D停止.以PQ为边在AB上方作正方形PQMN,设正方形PQMN与△ABC重叠部分的面积为S(cm2),点P运动的时间为t(s).
(1)当点N在边AC上时,求t的值.
(2)用含t的代数式表示PQ的长.
(3)当点Q沿D→B运动,正方形PQMN与△ABC重叠部分图形是五边形时,求S与t之间的函数关系式.
(4)直接写出正方形PQMN与△ABC重叠部分图形是轴对称图形时t的取值范围.

【答案】(1)![]() ;(2)3t或4-t;(3)
;(2)3t或4-t;(3)![]() <t≤
<t≤![]() 时,S=﹣
时,S=﹣![]() t2+10t﹣2;
t2+10t﹣2; ![]() ≤t<1时, S=﹣
≤t<1时, S=﹣![]() t2+6t;(4)0<t≤
t2+6t;(4)0<t≤![]() 或t=
或t=![]() .
.
【解析】试题分析:(1)由已知得出AD=BD=![]() AB=2,由正方形的性质得出PN=MN=MQ=PQ=3t,∠APN=∠QPN=∠PQM=∠NMQ=∠MNP=90°,由等腰直角三角形的性质得出∠A=∠B=45°,求出∠ANP=∠A=45°,得出AP=PN,即可得出答案;
AB=2,由正方形的性质得出PN=MN=MQ=PQ=3t,∠APN=∠QPN=∠PQM=∠NMQ=∠MNP=90°,由等腰直角三角形的性质得出∠A=∠B=45°,求出∠ANP=∠A=45°,得出AP=PN,即可得出答案;
(2)分两种情况:①当0<t≤1时,PQ=3t;②当1<t<2时,BQ=2t-2,求出DQ=4-2t,得出PQ=PD+DQ=4-t;
(3)分两种情况:①当![]() 时,QF=BQ=2-2t,ME=MF=5t-2,由正方形分面积减去等腰直角三角形的面积,即可得出答案;
时,QF=BQ=2-2t,ME=MF=5t-2,由正方形分面积减去等腰直角三角形的面积,即可得出答案;
②当![]() ≤t<1时,PG=AP=2-t,HQ=BQ=2-2t,由勾股定理得出AC=BC=
≤t<1时,PG=AP=2-t,HQ=BQ=2-2t,由勾股定理得出AC=BC=![]() ,由大等腰直角三角形的面积减去两个小等腰直角三角形的面积,即可得出答案;
,由大等腰直角三角形的面积减去两个小等腰直角三角形的面积,即可得出答案;
(4)分两种情况:①0<t≤![]() ;②AP=BQ,BQ=2t-2,AP=2-t,解方程求出
;②AP=BQ,BQ=2t-2,AP=2-t,解方程求出![]() 即可.
即可.
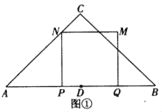
解:(1)如图①所示:
∵AB=4,点D是AB的中点,
∴AD=BD=![]() AB=2,
AB=2,
∵四边形ABCD是正方形,
∴PN=MN=MQ=PQ=3t,∠APN=∠QPN=∠PQM=∠NMQ=∠MNP=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∴∠ANP=∠A=45°,
∴AP=PN,
∴2﹣t=3t,
∴t=![]() ;
;
(2)分两种情况:
①当0<t≤1时,PQ=3t;
②当1<t<2时,BQ=2t﹣2,
∴DQ=2﹣(2t﹣2)=4﹣2t,
∴PQ=PD+DQ=4﹣t;
(3)分两种情况:
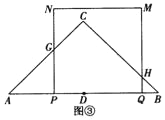
①当![]() <t≤
<t≤![]() 时,如图②所示:
时,如图②所示:
QF=BQ=2﹣2t,ME=MF=3t﹣(2﹣2t)=5t﹣2,
∴S=(3t)2﹣![]() (5t﹣2)2=﹣
(5t﹣2)2=﹣![]() t2+10t﹣2;
t2+10t﹣2;
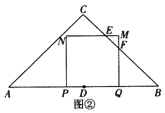
②当![]() ≤t<1时,如图③所示:
≤t<1时,如图③所示:
PG=AP=2﹣t,HQ=BQ=2﹣2t,
∵AC=BC=![]() AB=2
AB=2![]() ,
,
∴S=![]() ×(2
×(2![]() )2﹣
)2﹣![]() ×(2﹣t)2﹣
×(2﹣t)2﹣![]() ×(2﹣2t)2=﹣
×(2﹣2t)2=﹣![]() t2+6t;
t2+6t;
(4)分两种情况:
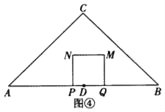
①如图④所示:此时0<t≤![]() ;
;
②如图⑤所示:
此时AP=BQ,BQ=2t﹣2,AP=2﹣t,
∴2﹣t=2t﹣2,
解得:t=![]() ;
;
综上所述:正方形PQMN与△ABC重叠部分图形是轴对称图形时t的取值范围为0<t≤![]() 或t=
或t=![]() .
.

【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产自行车
辆自行车,平均每天生产自行车![]() 辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入.下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负.单位:辆):
辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入.下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负.单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产自行车__________辆.
(2)产量最多的一天比产量最少的一天多生产__________辆.
(3)该厂实行按生产的自行车数量的多少计工资,即计件工资制.每生产一辆自行车可以得人民币![]() 元,若超额完成任务,则超出部分,每辆
元,若超额完成任务,则超出部分,每辆![]() 元;若不足计划数的,每少生产一辆扣
元;若不足计划数的,每少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.