题目内容
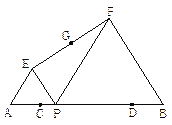
【题目】(1)如图①,△ABC是等边三角形,点D是边BC上任意一点(不与B、C重合),点E在边AC上,∠ADE=60°,∠BAD与∠CDE有怎样的数量关系,并给予证明.
(2)如图②,在△ABC中,AB=AC,点D是边BC上一点(不与B、C重合), ∠ADE=∠B,点E在边AC上.若CE=BD=3,BC=8,求AB的长度.

【答案】(1)见解析;(2)5
【解析】
(1)通过等边三角形以及角的换算即可证明;
(2)通过全等三角形和角的换算的相关性质,即可求出.
(1)∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
又∵∠ADE=60°,
∴∠BAD+∠BDA=∠BDA+∠EDC,
∴∠BAD=∠CDE
(2)∵△ABC中,AB=AC,
∴∠B=∠C
又∵∠ADE=∠B,
∴∠BAD=∠EDC
∵CE=BD,
∴△ABD≌△CDE(AAS)
∴AB=CD=BC-BD=8-3=5

练习册系列答案
相关题目
【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?