题目内容
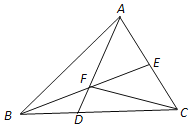
【题目】如图,D在△ABC的边BC上,DC=2BD,连接AD与△ABC的中线BE交于点F,连接CF,若△ABC的面积为24,则△AEF的面积为( )

A.4B.5C.6D.7
【答案】C
【解析】
可设S△BDF=x,由DC=2BD得S△CDF=2x. 由E是AC的中点,得S△ABE=S△CBE,S△AFE=S△CFE,进一步可得S△ABF=S△CBF=S△BDF+S△CDF=3x,于是S△ABD =4x,所以S△ACD=8x,所以S△ABC=S△ABD+S△ACD=12x. 由S△ABC=24可得方程12x=24,解出x=2,进一步即可求出结果.
解:设S△BDF=x,∵DC=2BD,∴S△CDF=2S△BDF=2x.
∵E是AC的中点,∴S△ABE=S△CBE,S△AFE=S△CFE,
∴S△ABE-S△AFE=S△CBE-S△CFE,
即S△ABF=S△CBF=S△BDF+S△CDF=3x,
∴S△ABD=S△ABF+S△BDF=4x,
∴S△ACD=2S△ABD=8x,
∴S△ABC=S△ABD+S△ACD=12x.
∵S△ABC=24,∴12x=24,解得x=2,∴S△ABF=6.
∵S△ABE=![]() S△ABC=12,
S△ABC=12,
∴S△AEF=S△ABE-S△ABF=12-6=6.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目