题目内容
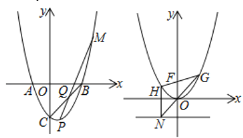
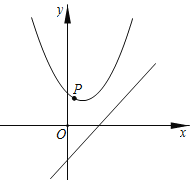
【题目】已知,抛物线y=![]() x2﹣x+2与直线y=x﹣2的图象如图,点P是抛物线上的一个动点,则点P到直线y=x﹣2的最短距离为( )
x2﹣x+2与直线y=x﹣2的图象如图,点P是抛物线上的一个动点,则点P到直线y=x﹣2的最短距离为( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
【答案】D
【解析】
设过点P平行直线y=x﹣2的解析式为y=x+b,当直线y=x+b与抛物线只有一个交点时,点P到直线y=x﹣2的距离最小,设直线y=x﹣2交x轴于A,交y轴于B,解直角三角形求得AB,然后根据等腰直角三角形的性质即可求得OC的长即可解决问题;
解:设过点P平行直线y1的解析式为y=x+b,
当直线y=x+b与抛物线只有一个交点时,点P到直线的距离最小,
由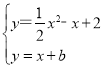 ,消去y得到:x2﹣4x+4﹣2b=0,
,消去y得到:x2﹣4x+4﹣2b=0,
当△=0时,4﹣8b=0,
∴b=0,
∴直线的解析式为y=x,
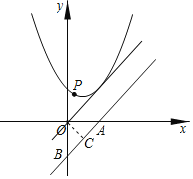
如图作OC⊥AB于C,
直线y=x﹣2交x轴于A,交y轴于B,则A(2,0),B(0,2),
∴OA=OB=2,
∴AB=2![]() ,
,
∵OC⊥AB,
∴AC=BC,
∴OC=![]() AB=
AB=![]() ,
,
故选:D.

练习册系列答案
相关题目