Question

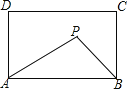
【题目】如图，四边形ABCD中，AC平分∠DAB，AD＝3，AC＝，DC＝，且∠ADC+∠ACB＝180°，则AB的长为_____．

Answer 1

【答案】

【解析】

过C作CE⊥AD于E，CF⊥AB于F，由角平分线的性质得出CE＝CF，证明Rt△ACE≌Rt△ACF（HL），得出AE＝AF，设CE＝CF＝x，DE＝y，则AE＝AF＝3+y，由勾股定理得出方程组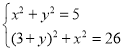，解方程组得出CE＝CF＝1，DE＝2，由三角函数得出tan∠CDE＝＝，作BG作AC于G，求出∠ACB＝∠CDE，得出tan∠ACB＝＝，设BG＝a，则CG＝2a，由三角形面积得出AB＝＝a，由勾股定理求出AG＝＝5a，得出方程5a+2a＝，得出a＝，即可得出答案．

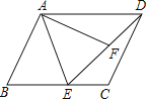
过C作CE⊥AD于E，CF⊥AB于F，如图所示：

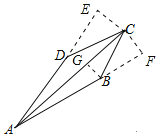
则∠AEC＝∠AFC＝90°，

∵AC平分∠DAB，

∴CE＝CF，

在Rt△ACE和Rt△ACF中，，

∴Rt△ACE≌Rt△ACF（HL），

∴AE＝AF，

设CE＝CF＝x，DE＝y，则AE＝AF＝3+y，

由勾股定理得：CE2+DE2＝CD2，AE2+CE2＝AC2，

∴，

解得：，或（舍去），

∴CE＝CF＝1，DE＝2，

∴tan∠CDE＝＝，

作BG作AC于G，

∵∠ADC+∠ACB＝180°，∠ADC+∠CDE＝180°，

∴∠ACB＝∠CDE，

∴tan∠ACB＝＝，

设BG＝a，则CG＝2a，

∵△ABC的面积＝AC×BG＝AB×CF，

∴AB＝＝a，

由勾股定理得：AG＝＝＝5a，

∵AG+CG＝AC＝，

∴5a+2a＝，

解得：a＝，

∴AB＝×＝；

故答案为：．