Question

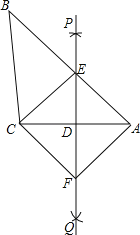
【题目】如图，已知△ABC，直线PQ垂直平分AC，与边AB交于点E，连接CE，过点C作CF∥BA交PQ于点F，连接AF．

（1）求证：△AED≌△CFD；

（2）求证：四边形AECF是菱形．

（3）若ED＝6，AE＝10，则菱形AECF的面积是多少？

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）96

【解析】

（1）由PQ为线段AC的垂直平分线得到AE＝CE，AD＝CD，然后根据CF∥AB得到∠EAC＝∠FCA，∠CFD＝∠AED，利用ASA证得两三角形全等即可；

（2）根据全等得到AE＝CF，然后根据EF为线段AC的垂直平分线，得到EC＝EA，FC＝FA，从而得到EC＝EA＝FC＝FA，利用四边相等的四边形是菱形判定四边形AECF为菱形；

（3）由菱形的性质和勾股定理求出AD，得出AC的长，由菱形的面积公式即可得出结果．

（1）证明：∵PQ为线段AC的垂直平分线，

∴AE＝CE，AD＝CD，

∵CF∥AB，

∴∠EAC＝∠FCA，∠CFD＝∠AED，

在△AED与△CFD中，

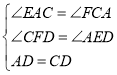
∴△AED≌△CFD（AAS）；

（2）证明：∵△AED≌△CFD，

∴AE＝CF，

∵EF为线段AC的垂直平分线，

∴EC＝EA，FC＝FA，

∴EC＝EA＝FC＝FA，

∴四边形AECF为菱形；

（3）解：∵四边形AECF是菱形，

∴AC⊥EF，

∵ED＝6，AE＝10，

∴EF＝2ED＝12，AD＝＝8．

∴AC＝2AD＝16，

∴菱形AECF的面积＝ACEF＝×16×12＝96．