题目内容
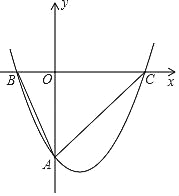
【题目】如图,经过点A(0,﹣4)的抛物线y=![]() x2+bx+c与x轴相交于点B(﹣2,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣2,0)和C,O为坐标原点.
(1)求抛物线解析式;
(2)将抛物线y=![]() x2+bx+c向上平移
x2+bx+c向上平移![]() 个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围.
个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围.
【答案】(1)y=![]() x2﹣x﹣4;(2)0<m<
x2﹣x﹣4;(2)0<m<![]() .
.
【解析】
(1)该抛物线的解析式中只有两个待定系数,只需将A、B两点坐标代入即可得解;
(2)首先根据平移条件表示出移动后的函数解析式,从而用m表示出该函数的顶点坐标,将其代入直线AB、AC的解析式中,即可确定P在△ABC内时m的取值范围.
(1)将A(0,﹣4)、B(﹣2,0)代入抛物线y=![]() x2+bx+c中,得:
x2+bx+c中,得:
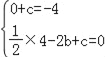 ,
,
解得:![]() ,
,
故抛物线的解析式:y=![]() x2﹣x﹣4.
x2﹣x﹣4.
(2)由题意,新抛物线的解析式可表示为:y=![]() (x+m)2﹣(x+m)﹣4+
(x+m)2﹣(x+m)﹣4+![]() ,即:y=
,即:y=![]() x2+(m﹣1)x+
x2+(m﹣1)x+![]() m2﹣m﹣
m2﹣m﹣![]() ;
;
它的顶点坐标P:(1﹣m,﹣1);
由(1)的抛物线解析式可得:C(4,0);
设直线AC的解析式为y=kx+b(k≠0),把x=4,y=0代入,
∴4k+b=0,b=﹣4,
∴y=x﹣4.
同理直线AB:y=﹣2x﹣4;
当点P在直线AB上时,﹣2(1﹣m)﹣4=﹣1,解得:m=![]() ;
;
当点P在直线AC上时,(1﹣m)﹣4=﹣1,解得:m=﹣2;
∴当点P在△ABC内时,﹣2<m<![]() ;
;
又∵m>0,
∴符合条件的m的取值范围:0<m<![]() .
.

练习册系列答案
相关题目