题目内容
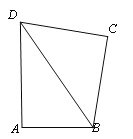
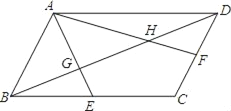
【题目】如图，在平行四边形ABCD中，E、F分别是BC边，CD边的中点，AE、AF分别交BD于点G，H，设△AGH的面积为S1，平行四边形ABCD的面积为S2，则S1：S2的值为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由平行可得
，
，从而得到对应线段成比例，推得BG=GH=DH，最后利用等底等高的三角形面积相等推理得解。
解：∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，AB=CD，AD=BC，
∴
,
,
,
同理，
,
∵DF=CF，BE=CE，
∴
,
∴
,
∴BG=GH=DH，
∵△AGH的面积为S1，
∴S△ABG=S△AGH=S△ADH=S1，
∴S平行四边形ABCD=6S1，
∴S1：S2，=1：6，
故选：A．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
【题目】为了提高学生书写汉字的能力，增强保护汉子的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为
（分），且
，将其按分数段分为五组，绘制出以下不完整表格：
组别 | 成绩 | 频数（人数） | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
请根据表格提供的信息，解答以下问题：
（1）本次决赛共有 名学生参加；
（2）直接写出表中a= ,b= ;
（3）请补全下面相应的频数分布直方图；
（4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为 。
