题目内容
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
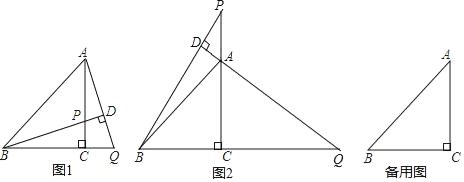
(1)如图1,当P在线段AC上时,求证:BP=AQ;
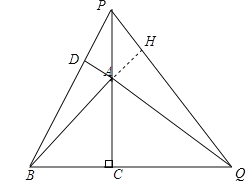
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA= 度时,存在AQ=2BD,说明理由.
【答案】(1)证明见解析;(2)(2)成立,理由见解析;(3)当∠DBA=22.5°时,存在AQ=2BD,理由见解析.
【解析】试题分析:(1)首先根据内角和定理得出∠DAP=∠CBP,进而得出
△ACQ≌△BCP即可得出答案;
(2)延长BA交PQ于H,由于![]() 得到
得到![]() 推出△AQC≌△BPC(ASA),即可得出结论;
推出△AQC≌△BPC(ASA),即可得出结论;
(3)当![]() 时,存在
时,存在![]() 根据等腰三角形的性质得到BP=2BD,通过△PBC≌△ACQ,根据全等三角形的性质即可得到结论.
根据等腰三角形的性质得到BP=2BD,通过△PBC≌△ACQ,根据全等三角形的性质即可得到结论.
试题解析:
(1)证明:∵∠ACB=∠ADB=90°,∠APD=∠BPC,
∴∠DAP=∠CBP,
在△ACQ和△BCP中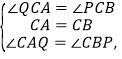
∴△ACQ≌△BCP(ASA),
∴BP=AQ
(2)成立,
理由:延长BA交PQ于H,
![]() ∠AQC=∠BQD,
∠AQC=∠BQD,
∴∠CAQ=∠DBQ,
在△AQC和△BPC中,
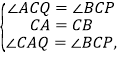
∴△AQC≌△BPC(ASA),
∴AQ=BP,
故答案为:成立;
(3)22.5°,
当∠DBA=22.5°时,存在AQ=2BD,
理由:∵∠BAC=∠DBA+∠APB=45°,
∴∠PBA=∠APB=22.5°,
∴AP=AB,
∵AD⊥BP,
∴BP=2BD,
在△PBC与△QAC中,
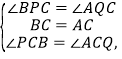
∴△PBC≌△ACQ,
∴AQ=PB,
∴AQ=2BD.
故答案为:22.5°.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目