题目内容
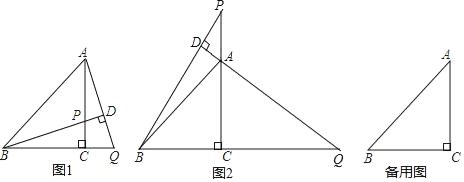
【题目】如图,在长方形ABCD中,AB=8cm,BC=6cm,点E是CD边上的一点,且DE=2cm,动点P从A点出发,以2cm/s的速度沿A→B→C→E运动,最终到达点E.当△APE的面积等于20cm2时,求点P运动的时间.
【答案】当t=![]() s或6s时,△APE的面积等于20cm2.
s或6s时,△APE的面积等于20cm2.
【解析】试题分析:分为三种情况讨论,如图1,当点P在AB上,即0<t≤4时,根据三角形的面积公式建立方程求出其解即可;如图2,当点P在BC上,即4<t≤7时,由S△APE=S四边形AECB-S△PCE-S△PAB建立方程求出其解即可;如图3,当点P在EC上,即7<t≤10时,由S△APE=![]() =20建立方程求出其解即可.
=20建立方程求出其解即可.
试题分析:设点P运动的时间为t s,
∵四边形ABCD是矩形,
∴AD=BC=6,AB=CD=8,
如图1,当点P在AB上,即0<t≤4时,此时AP=2t,S△APE=![]() ×2t×6=20,解得t=
×2t×6=20,解得t=![]() (s);
(s);
如图2,当点P在BC上,即4<t≤7时,此时BP=2t-8,CP=8+6-2t=14-2t,S△APE=48-S△ADE-S△ABP-S△PCE,
即20=48-![]() ×6×2-
×6×2-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×6×(14-2t),
×6×(14-2t),
解得:t=6(s);
如图3,当点P在EC上,即7<t≤10时,此时PE=8+6+8-2-2t=20-2t,S△APE=![]() =
=![]() ×6×(20-2t)=20,
×6×(20-2t)=20,
解得t=![]() (s),
(s),
∵![]() <7,∴t=
<7,∴t=![]() 应舍去;
应舍去;
综上所述,当t=![]() s或6s时,△APE的面积等于20cm2.
s或6s时,△APE的面积等于20cm2.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目