题目内容
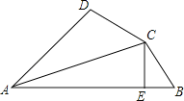
【题目】在△ABC和△ADE中,AB=AC,∠BAC=120°,∠ADE=90°,∠DAE=60°,F为BC中点,连接BE、DF,G、H分别为BE,DF的中点,连接GH.
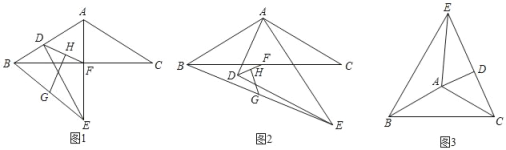
(1)如图1,若D在△ABC的边AB上时,请直接写出线段GH与HF的位置关系 ,![]() = .
= .
(2)如图2,将图1中的△ADE绕A点逆时针旋转至图2所示位置,其它条件不变,(1)中结论是否改变?请说明理由;
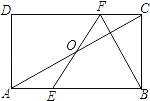
(3)如图3,将图1中的△ADE绕A点顺时针旋转至图3所示位置,若C、D、E三点共线,且AE=2,AC=![]() ,请直接写出线段BE的长 .
,请直接写出线段BE的长 .
【答案】(1)GH⊥HF,![]() ;(2)结论不变;(3)
;(2)结论不变;(3)![]() .
.
【解析】
(1)如图1中,连接DG,FG.根据直角三角形斜边中线的性质,可得GD=GF,再证明△DGF是等边三角形即可解决问题;
(2)结论不变.如图2中,延长ED至S,使DS=DE,连接AS,BS,CE,FG,DG.理由三角形的中位线定理,证明GD=GF,△GDF是等边三角形即可解决问题;
(3)如图3中,延长ED到H,使得DH=DE,连接AH,BH,作BM⊥EC于M,设BC交AH于点O.想办法证明∠BHE=60°,解直角三角形求出BM,ME即可解决问题;
解:(1)如图1中,连接DG,FG.
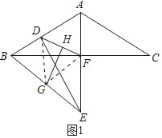
∵AB=AC,BF=CF,
∴AF⊥ BC,∴ ∠ BAF= ∠ CAF=60°,
∵ ED⊥ AB,
∴ ∠ BFE=∠ BDE=90°,
∵BG=GE,
∴DG=![]() BE,GF=
BE,GF=![]() BE,
BE,
∴DG=FG,∵DH=HF,
∴GH⊥ DF,
∵ ∠ BAE=60°,
∴ ∠ ABE+∠ AEB=120°,
∵ DG=BG=GF=GE,
∴ ∠ GBD=∠ GDB,∠ GEF=∠GFE,
∴ ∠ BGD+∠ EGF=120°,
∴ ∠ DGF=60°,
∴ △ DGF是等边三角形,
∴![]() =tan60°=
=tan60°=![]() .
.
故答案为GH⊥ HF,![]() =
=![]() .
.
(2)结论不变.
理由:如图2中,延长ED至S,使DS=DE,连接AS,BS,CE,FG,DG.
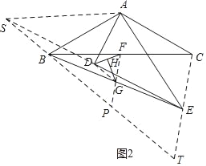
∵ ∠ ADE=90°
∴ AS=AE,∠DAE=∠DAS=60°
∴ ∠ BAC=∠SAE=120°
∴ ∠ SAB= ∠ EAC
∵AB=AC
∴ △ ABS ≌ △ ACE
∴ BS=CE,∠ ABS=∠ACE
∵F,G分别为BC,BE中点
∴FG∥CE,FG=![]() CE,
CE,
同理:DG∥BS,DG=![]() BS,
BS,
∴DG=FG,
∵H为DF中点,
∴ GH⊥ HF,
延长SB交CE延长线于T,
∵ ∠ ABS+∠ABT=∠ ACE+∠ ABT=180°,
∴ ∠ BAC+∠ T=120°,
∴ ∠ T=60°,
延长FG交BT于P,
∴ ∠ T=∠ BPF=∠ DGF=60°,
∴ ∠HGF=30°,
∴ ![]() =
=![]() .
.
(3)如图3中,延长ED到H,使得DH=DE,连接AH,BH,作BM⊥EC于M,设BC交AH于点O.
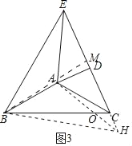
∵AD⊥EH,ED=DH,
∴AE=AH,
∴∠AEH=∠AHE=30°,
∴∠EAH=∠BAC=120°,
∴∠BAH=∠CAE,
∵AB=AC,AH=AE,
∴△BAH ≌ △ CAE(SAS),
∴ ∠ BHA=∠ AEC=30°,BH=CE,
∴∠ OBA=∠OHC=30°,
∵∠AOB=∠COH,
∴△AOB ∽ △COH,
∴ ![]() =
=![]() ,
,
∴ ![]() ,∵∠ AOC=∠ BOH,
,∵∠ AOC=∠ BOH,
∴ △ AOC∽ △ BOH,
∴∠BHO=∠AOC=30°,
∴∠BHE=30°+30°=60°,
在Rt△ADE中,∵AE=2,∠ AED=30°,
∴AD=1,ED=DH=![]() ,
,
在Rt△ADC中,CD=![]() =
=![]() ,
,
∴BH=EC=2![]()
![]() ,
,
在Rt△BMH中,HM=![]() (2+
(2+![]() ),BM=
),BM=![]() HM=
HM=![]() (2
(2![]() +3),
+3),
∴EM=EH﹣HM=2![]() ﹣
﹣![]() (2+
(2+![]() )=
)=![]()
![]() ﹣1,
﹣1,
在Rt△EBM中,BE=![]() =
=![]() =
=![]() .
.
故答案为![]() .
.