Question

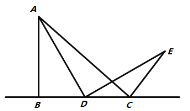
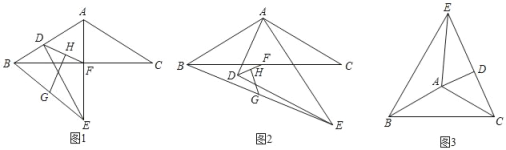
【题目】将两块全等的含30°角的三角尺按如图1所示的方式摆放在一起，它们较短的直角边BC＝EC＝3．

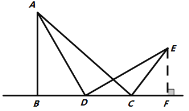
（1）将△ECD沿直线l向左平移到图2的位置，使点E′落在AB上，则CC′＝　 　；

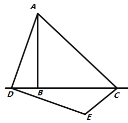
（2）将△ECD绕点C逆时针旋转到图3的位置，使点E′落在AB上，则△ECD绕点C旋转的度数为　 　；

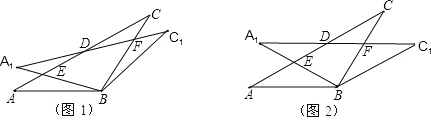
（3）将△ECD沿直线AC翻折到图4的位置，ED′与AB相交于点F，求证：AF＝FD′．

Answer 1

【答案】（1）3﹣；（2）30°；（3）见解析

【解析】

（1）先判断出C'E'＝3，再利用含30度角的直角三角形的性质得出BE'＝2BC，最后用勾股定理求出BC'即可得出结论；

（2）△ECD绕点C旋转的度数即∠ECE'的度数；易得：∠ECE′＝∠BAC＝30°；

（3）根据条件，证明△AEF≌△D′BF进而得出AF＝FD′.

解：（1）解：CC′＝3﹣．

理由如下：由平移知，C'E'∥AC，C'E'＝CE＝3，

∴∠BE'C'＝∠A＝30°，

∵BC＝EC＝3，

在Rt△BC'E'中，∠BE'C'＝30°，

根据在直角三角形中，30°角所对的直角边是斜边的一半，得BE'＝2BC'

∴BE'2﹣BC'2＝C'E'2，

即：4BC'2﹣BC'2＝9，

∴BC'＝，

∴CC′＝BC﹣BC'＝3﹣；

故答案为：3﹣；

（2）解：△ECD绕点C旋转的度数即∠ECE′的度数；

∵∠ABC＝60°，BC＝CE′＝3，AB＝6，

∴△E′BC是等边三角形，

∴BC＝E′C＝E′B＝3，

∴AE′＝E′C＝3，

∴∠E′AC＝∠E′CA，

∴∠ECE′＝∠BAC＝30°；

故答案为：30°；

（3）证明：∵AE＝AC﹣EC，D′B＝D′C﹣BC，

又∵AC＝D′C，EC＝BC，

∴AE＝D′B，

又∵∠AEF＝∠D′BF＝180°﹣60°＝120°，∠A＝∠CD′E＝30°，

在△AEF和△D′BF中，

，

∴△AEF≌△D′BF（ASA），

∴AF＝FD'.