题目内容
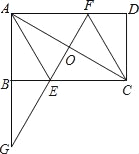
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为_________.
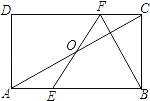
【答案】6
【解析】
先证明△AOE≌△COF,Rt△BFO≌Rt△BFC,再证明△OBC、△BEF是等边三角形即可求出答案.
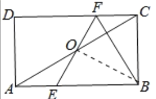
如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO
在△AOE与△COF中,
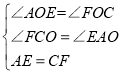
∴△AOE≌△COF
∴OE=OF,OA=OC
∵BF=BE
∴BO⊥EF,∠BOF=90°
∵∠BEF=2∠BAC=∠CAB+∠AOE
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2
在Rt△BFO与Rt△BFC中
![]()
∴Rt△BFO≌Rt△BFC
∴BO=BC
在Rt△ABC中,∵AO=OC,
∴BO=AO=OC=BC
∴△BOC是等边三角形
∴∠BCO=60°,∠BAC=30°
∴∠FEB=2∠CAB=60°,
∵BE=BF
∴EB=EF=4
∴AB=AE+EB=2+4=6,
故答案为6.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c,如表给出了y与x的部分对应值:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | n | 3 | 0 | ﹣5 | ﹣12 | … |
(1)根据表格中的数据,试确定二次函数的解析式和n的值;
(2)抛物线y=ax2+bx+c与直线y=2x+m没有交点,求m的取值范围.