��Ŀ����
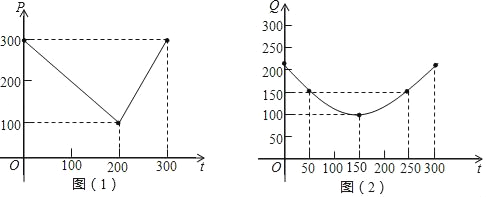
����Ŀ����7�֣�ij�߲˻�����ֲ���������������г������֪����2��1�����300���ڣ��������г��ۼ�������ʱ��Ĺ�ϵ��ͼ��1����һ�����߱�ʾ������������ֲ�ɱ�������ʱ��Ĺ�ϵ��ͼ��2���������߶�Q=![]() ��t��150��2+100 ��0��t��300����ʾ����ע���г��ۼۺ���ֲ�ɱ��ĵ�λ��Ԫ/100kg��ʱ�䵥λ���죩
��t��150��2+100 ��0��t��300����ʾ����ע���г��ۼۺ���ֲ�ɱ��ĵ�λ��Ԫ/100kg��ʱ�䵥λ���죩
��1��д��ͼ��1����ʾ���г��ۼ�P��ʱ��t�ĺ�����ϵʽ��
��2���϶��г��ۼۼ�ȥ��ֲ�ɱ�Ϊ�����棬�ʺ�ʱ���е����������������
���𰸡���1��P=![]() ����2���Ӷ���һ�տ�ʼ�ĵ�50�����д��������
����2���Ӷ���һ�տ�ʼ�ĵ�50�����д��������
��������
�ɴ�����=����-�ɱ�, ��ϴӶ���һ�����300����, �������г��ۼ�P������ʱ��t�����ϵ P=![]() ,����������ֲ�ɱ�Q������ʱ��t�����ϵQ=
,����������ֲ�ɱ�Q������ʱ��t�����ϵQ=![]() ��t��150��2+100(0��t��300), �����õ�������h(t) �Ľ���ʽ, ���ݷֶκ����ֶδ�����ԭ��, ���Ƿֱ���������Ϻ�������ֵ, �ۺ����۽��, ���ɵõ�����.
��t��150��2+100(0��t��300), �����õ�������h(t) �Ľ���ʽ, ���ݷֶκ����ֶδ�����ԭ��, ���Ƿֱ���������Ϻ�������ֵ, �ۺ����۽��, ���ɵõ�����.
��1����0��t��200ʱ�����г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=k1t+b1��
![]() ����
����![]() ��
��
����0��t��200ʱ���г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=��t+300��
��200��t��300ʱ�����г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=k2t+b2��
![]() ����
����![]() ��
��
����200��t��300ʱ���г��ۼ�P��ʱ��t�ĺ�����ϵʽΪP=2t��300��
���Ͽɵã�P=![]() ��
��
��2�����t��Ĵ�����ΪyԪ��
y=P��Q��
��0��t��200ʱ��y=����t+300����[![]() ��t��150��2+100]=
��t��150��2+100]=![]() ��
��
����t=50ʱ��yȡ�����ֵ����ʱy=100��
��200��t��300ʱ��y=��2t��300����[![]() ��t��150��2+100]=
��t��150��2+100]=![]() ��
��
��t=300ʱ��yȡ�����ֵ����ʱy=87.5��
���Ͽɵã��Ӷ���һ�տ�ʼ�ĵ�50�����д��������

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�