题目内容
如图，已知：在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，且a、b是关于x的一元二次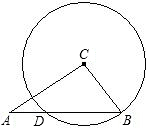
方程x2+4（c+2）=（c+4）x的两个根，点D是以C为圆心，CB为半径的圆与AB的交点．
（1）证明：△ABC是直角三角形；
（2）若
=
，求AB的长；
（3）在（2）的条件下求AD长．
方程x2+4（c+2）=（c+4）x的两个根，点D是以C为圆心，CB为半径的圆与AB的交点．（1）证明：△ABC是直角三角形；
（2）若
| a |
| b |
| 3 |
| 4 |
（3）在（2）的条件下求AD长．
（1）证明：依题意，得a+b=c+4，ab=4（c+2）（1分）
∴a2+b2=（a+b）2-2ab=（c+4）2-2×4（c+2）=c2+8c+16-8c-16=c2
∴△ABC是直角三角形．（3分）
（2）设a=3k，b=4k，从而c=5k（k＞0）．
代入a+b=c+4，得k=2；
∴a=6，b=8，c=10．（5分）
（3）过C作CE⊥AB于E．
则CE=
=
，BE=
=
=
；
由垂径定理，得BD=2BE=
；
故AD=10-BD=10-7.2=2.8．（9分）
∴a2+b2=（a+b）2-2ab=（c+4）2-2×4（c+2）=c2+8c+16-8c-16=c2
∴△ABC是直角三角形．（3分）
（2）设a=3k，b=4k，从而c=5k（k＞0）．
代入a+b=c+4，得k=2；
∴a=6，b=8，c=10．（5分）
（3）过C作CE⊥AB于E．
则CE=
| ab |
| c |
| 24 |
| 5 |
| BC2-CE2 |
62-(
|
| 18 |
| 5 |
由垂径定理，得BD=2BE=
| 36 |
| 5 |
故AD=10-BD=10-7.2=2.8．（9分）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
