题目内容
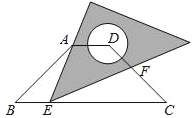
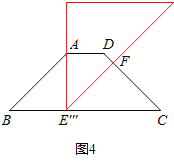
【题目】如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4![]() ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
【答案】2,4![]() ﹣3,
﹣3,![]()
【解析】分析:首先理解题意,得出此题应该分三种情况进行分析,分别是AB=AE,AB=BE,AE=BE,从而得到最后答案.
详解:作AM⊥BC,DN⊥BC,
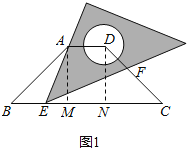
根据已知条件可得,BM=(BC-AD)÷2,
在直角三角形ABM中,cosB=![]() ,
,
则AB=(BC-AD)÷2÷cosB=3,
①当AB=AE′时,如图,
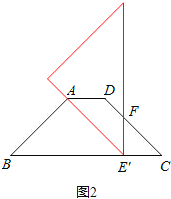
∠B=45°,∠AE′B=45°,
∴AE′=AB=3,
则在Rt△ABE′中,BE′=![]() ,
,
故E′C=4![]() -3
-3![]() =
=![]() .
.
易得△FE′C为等腰直角三角形,
故CF=![]() =2.
=2.
②当AB=BE″时,
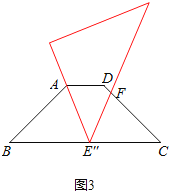
∵AB=3,
∴BE″=3,
∵∠AE″B=∠BAE″=(180°-45°)÷2=67.5°,
∴∠FE″C=180°-45°-67.5°=67.5°,
∴∠CFE″=180°-∠C-∠FE″C=67.5°,
∵△E″CF为等腰三角形,
∴CF=CE″=CB-BE″=4![]() -3;
-3;
③当AE=BE′″时,△ABE′″和△CFE′″是等腰Rt△,
∴BE′″=![]() ,
,
∴CE′″=![]()
∴CF=FE′″=![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目