��Ŀ����
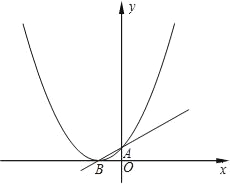
����Ŀ����֪������y=ax2+x+1��ͼ����x��ֻ��һ�������㣮
��1�������������ϵʽ��
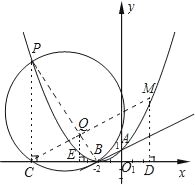
��2����ͼ��ʾ������κ���y=ax2+x+1ͼ��Ķ���ΪB����y��Ľ���ΪA��PΪͼ���ϵ�һ�㣬�����߶�PBΪֱ����Բ��ֱ��AB�����ڵ�B����P������ꣻ
��3���ڣ�2���У���Բ��x����һ�������ֱ��PB�ĶԳƵ�ΪM����̽����M�Ƿ���������y=ax2+x+1�ϣ������������ϣ����M������ꣻ�����ڣ���˵�����ɣ�
���𰸡���1��y=x+1��y=![]() x2+x+1����2��P�������Ϊ������10��16������3����M����������y=ax2+x+1��
x2+x+1����2��P�������������10��16������3����M����������y=ax2+x+1��
����������������1������Ӧ�������������a=0���˺�����һ�κ�������x��ֻ��һ�����㣻
��a��0���˺����Ƕ��κ��������ɸ����б�ʽ���a��ֵ���Դ�ȷ�������ʽ��
��2����Բ��x�����һ������ΪC������PC����Բ�ܽǶ���֪PC��BC������PB��Բ��ֱ������AB��Բ��B����PB��AB���ɴ˿�֤����PBC�ס�BAO�������������������εĶ�Ӧֱ�DZ߳ɱ��������ɵõ�PC��BC�ı�����ϵ���ɸ������������ϵ����P������꣬���������ߵĽ���ʽ�������P������ꣻ
��3������CM����CM��PB�Ľ���ΪQ������C��M����ֱ��PB�Գƣ���ôPB��ֱƽ��CM����CQ=QM����M��MD��x����D��ȡCD���е�E������QE����QE��Rt��CMD����λ�ߣ���Rt��PCB�У�CQ��OB��QE��BC����֤�á�BQE����QCE���͡�CPQ��ȣ�������ǵ�����ֵ������![]() ���ڣ�2�����Ѿ���ã����ɴ˿ɵõ�CE=2QE=4BE����2�����Ѿ������CB�ij�������CE��BE�ı�����ϵ���������BE��CE��QE�ij����ɴ˿ɵõ�Q�����꣬Ҳ�͵õ�M������꣬Ȼ��M���������ߵĽ���ʽ�н����жϼ��ɣ�
���ڣ�2�����Ѿ���ã����ɴ˿ɵõ�CE=2QE=4BE����2�����Ѿ������CB�ij�������CE��BE�ı�����ϵ���������BE��CE��QE�ij����ɴ˿ɵõ�Q�����꣬Ҳ�͵õ�M������꣬Ȼ��M���������ߵĽ���ʽ�н����жϼ��ɣ�
��⣺��1����a=0ʱ��y=x+1��ͼ����x��ֻ��һ��������
��a��0ʱ����=1��4a=0��a=![]() ����ʱ��ͼ����x��ֻ��һ�������㣮
����ʱ��ͼ����x��ֻ��һ�������㣮
�ຯ���Ľ���ʽΪ��y=x+1��y=![]() x2+x+1��
x2+x+1��
��2����PΪ���κ���ͼ���ϵ�һ�㣬����P��PC��x���ڵ�C��
��y=ax2+x+1�Ƕ��κ������ɣ�1��֪�ú�����ϵʽΪ��
y=![]() x2+x+1��
x2+x+1��
�ඥ��ΪB����2��0����ͼ����y��Ľ���
����ΪA��0��1��
����PBΪֱ����Բ��ֱ��AB�����ڵ�B
��PB��AB���PBC=��BAO
��Rt��PCB��Rt��BOA
��![]() ����PC=2BC��
����PC=2BC��
��P���������x��y����
�ߡ�ABO����ǣ���PBA��ֱ�ǣ�
���PBO�Ƕ۽ǣ�
��x����2
��BC=��2��x��PC=��4��2x��
��y=��4��2x��P���������x����4��2x��
�ߵ�P�ڶ��κ���y=![]() x2+x+1��ͼ���ϣ�
x2+x+1��ͼ���ϣ�
����4��2x=![]() x2+x+1
x2+x+1
��֮�ã�x1=��2��x2=��10
��x����2��
��x=��10��
��P�������������10��16��
��3����M����������y=ax2+x+1��
�ɣ�2��֪��CΪԲ��x�����һ���㣬����CM��CM��ֱ��PB�Ľ���ΪQ������M��x��Ĵ��ߣ�����ΪD��ȡCD���е�E������QE����CM��PB����CQ=MQ����QE����λ�ߣ�
��QE��MD��QE=![]() MD��QE��CE
MD��QE��CE
��CM��PB��QE��CE��PC��x��
���QCE=��EQB=��CPB
��tan��QCE=tan��EQB=tan��CPB=![]()
CE=2QE=2��2BE=4BE����CB=8��
��BE=![]() ��QE=
��QE=![]()
��Q�����������![]() ��
��![]() ��
��
�����M���������![]() ��
��![]() ��
��
��![]()
��C�����ֱ��PB�ĶԳƵ�M����������y=ax2+x+1�ϣ�

 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д� Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�����Ŀ����20��ײˣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�
��������IJ�ֵ����λ��ǧ�ˣ� |
|
|
| 0 | 1 | 2.5 |
���� | 1 | 4 | 2 | 3 | 2 | 8 |
��1��20��ײ��У����ص�һ��������һ����ض���ǧ�ˣ�
��2����������Ƚϣ�20��ײ��ܼƳ����������ǧ�ˣ�
��3�����ײ�ÿǧ���ۼ�2.8Ԫ���������20��ײ˿�������Ԫ�����������������