题目内容
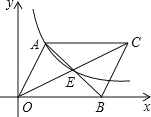
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列关系式不正确的是（ ） 
A.abc＜0
B.a+b+c＜0
C.2a﹣b＞0
D.4a﹣b+c＜0
【答案】C
【解析】解：由函数图象可得各系数的关系：a＜0，b＜0，c＞0，
∵a＜0，b＜0，c＞0，
∴abc＜0，故A错误；
∵x=1时，y＜0，
∴a+b+c＜0，故B错误；
∵对称轴x=﹣ 
=﹣1，
∴b=2a，
∴2a﹣b=0，故C正确；
∵x=﹣2时，y＜0，
∴4a﹣2b+c＜0，故C错误．
故选C．
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
练习册系列答案
相关题目
【题目】某商店一周内甲、乙两种计算器每天的销售量如下（单位：个）：
类别/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均数 |
甲 |
|
|
|
|
|
|
| |
乙 |
|
|
|
|
|
|
|
|
（1）将表格填写完整．
（2）求甲种计算器本周销售量的方差．
（3）已知乙种计算器本周销售量的方差为
，本周哪种计算器的销售量比较稳定？说明理由．
