题目内容
【题目】已知:抛物线y=x2+(b﹣1)x﹣5.
(1)写出抛物线的开口方向和它与y轴交点的坐标;
(2)若抛物线的对称轴为直线x=1,求b的值,并画出抛物线的草图(不必列表);
(3)如图,若b>3,过抛物线上一点P(﹣1,c)作直线PA⊥y轴,垂足为A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数解析式.
【答案】
(1)
解:∵a=1>0,
∴抛物线开口向上,
当x=0时,y=02+(b﹣1)×0﹣5=﹣5,
∴它与y轴的交点坐标为(0,﹣5)
(2)
解:抛物线的对称轴为x=1,
∴﹣ ![]() =﹣
=﹣ ![]() =1,
=1,
解得b=﹣1,
故抛物线的解析式为y=x2﹣2x﹣5;
图象如下:
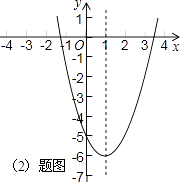
(3)
解:∵b>3,
∴抛物线的对称轴x=﹣ ![]() =﹣
=﹣ ![]() <﹣1,
<﹣1,
∴对称轴在点P的左侧,
∵直线PA⊥y轴,且P(﹣1,c),BP=2PA,
∴点B的坐标为(﹣3,c),
把点B(﹣3,c)、P(﹣1,c)代入抛物线解析式y=x2+(b﹣1)x﹣5得,
![]() ,
,
解得 ![]() ,
,
∴抛物线所对应的二次函数解析式为y=x2+4x﹣5;
[或:∵点B(﹣3,c)、P(﹣1,c),
∴BP的中点(﹣2,c)在抛物线的对称轴上,
∴﹣ ![]() =﹣
=﹣ ![]() =﹣2,解得b=5.]
=﹣2,解得b=5.]
【解析】(1)根据a值大于0,判断抛物线的开口向上,令x=0求出函数值y,就是抛物线与y轴的交点坐标;(2)根据对称轴解析式列式求出b的值,从而得到抛物线解析式,再根据抛物线与坐标轴的交点与顶点坐标作出草图即可;(3)先根据b>3判断出点P在对称轴的左侧,然后根据BP=2PA求出点B的坐标,然后把点P、B的坐标代入抛物线解析式,利用待定系数法求出b、c的值,即可写出该抛物线对应的二次函数解析式.[或者根据点BP的中点在抛物线的对称轴上,利用对称轴解析式列式进行计算求解b的值.]
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费=自来水销售费用+污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
17吨及以下 | a | 0.80 |
超过17吨不超过30吨的部分 | b | 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a,b的值.
(2)小王家6月份交水费184元,则小王家6月份用水多少吨?
【题目】颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的面积是米2 .
【题目】某商店一周内甲、乙两种计算器每天的销售量如下(单位:个):
类别/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均数 |
甲 |
|
|
|
|
|
|
| |
乙 |
|
|
|
|
|
|
|
|
(1)将表格填写完整.
(2)求甲种计算器本周销售量的方差.
(3)已知乙种计算器本周销售量的方差为![]() ,本周哪种计算器的销售量比较稳定?说明理由.
,本周哪种计算器的销售量比较稳定?说明理由.