题目内容
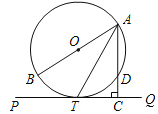
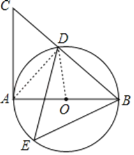
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,
,![]() 是
是![]() 上一点,且与点
上一点,且与点![]() 在
在![]() 异侧,连结
异侧,连结![]()
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]() 的长为(结果保留
的长为(结果保留![]() )
)
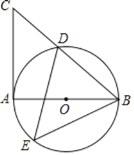
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AD,易得∠ADB=90°,∠BAC=90°,根据余角的性质,可得∠DAB=∠C,结合圆周角定理,即可得到结论;
(2)连接OD,由圆周角定理得∠BOD=100°,根据弧长公式,即可求解.
(1)连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵AC切⊙O于点A,
∴CA⊥AB,
∴∠BAC=90°,
∴∠C+∠ABD=90°,
又∵∠DAB+∠ABD=90°,
∴∠DAB=∠C,
∵∠DAB=∠BED,
∴∠C=∠BED;
(2)连接OD,
∵∠BED=∠C=50°,
∴∠BOD=2∠BED=100°,
∴![]() 的长度=
的长度=![]() =
=![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目