题目内容
【题目】已知O为坐标原点，抛物线y＝x2﹣3x﹣4与x轴交于A，B两点（点A在点B的右侧），有点C(﹣2，6)．
（1）求A，B两点的坐标．
（2）若点D(1，﹣3)，点E在线段OA上，且∠ACB＝∠ADE，延长ED交y轴于点F，求△EFO的面积．
（3）若M在直线AC上，点Q在抛物线上，是否存在点M和点N，使以Q，M，N，A为顶点的四边形是正方形？若存在，直接写出M点的坐标．若不存在，请说明理由．
【答案】（1）A(4，0)，B(﹣1，0)；（2）
；（3）存在，
或M(0，4)或M(8，﹣4)
【解析】
（1）令x2﹣3x﹣4＝0求出解即可求点的坐标；
（2）过点B作BG⊥AC，过点
作
，设E（m，0），由△ABC、△ADE的面积可求
、 
，因为根据相似三角形的性质求出m的值，确定E、F点坐标即可求；
（3）当AC为正方形QAMN边时，M点与N点关于x轴对称；M、N的中点与A、Q中点相同可求M的坐标；当M、Q关于x轴对称时，M（0，4），此时Q（0，﹣4）在抛物线上；当Q（0，﹣4）时，M（8，﹣4）．
解：（1）令x2﹣3x﹣4＝0，解得x＝4或x＝﹣1，
∵点A在点B的右侧
∴A（4，0），B（﹣1，0）；
（2）过点B作BG⊥AC，过点作，如图：
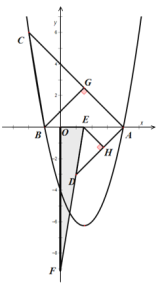
设E（m，0），
∵C（﹣2，6），D（1，﹣3），
AC＝ 
，AD＝
，BC＝
由△ABC的面积可得
∴
由△ADE的面积可得，
∴
∵∠ACB＝∠ADE，
∴
∴
∴
∴2m2﹣41m+57＝0
∴
或m＝19
∵点E在线段OA上
∴
∵设ED的直线解析式为
，，
∴
∴
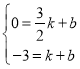
∴ED的直线解析式为
∴当
时，
∴
∴
（3）设
的直线解析式为，
，
∴
∴
∴直线的解析式为
∵
∴∠CAO＝45°，
设M（t，﹣t+4），
①当M点与N点关于x轴对称时，如图：
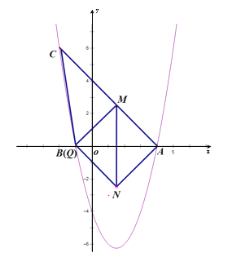
∴N（t，t﹣4），
∴M、N的中点为（t，0），
∴A、Q中点也为（t，0），
∴Q（2t﹣4，0），
∵点Q在抛物线上，
∴2t﹣4＝﹣1，
∴
∴
②当M、Q关于x轴对称时，M（0，4），此时Q（0，﹣4）在抛物线上，如图：
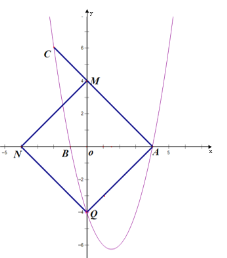
③当Q（0，﹣4）时，M（8，﹣4），如图：
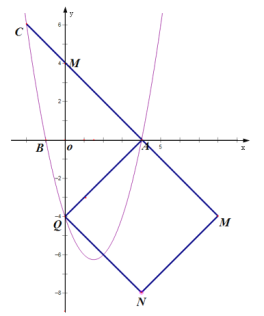
∴综上所述：或M（0，4）或M（8，﹣4）．
故答案是：（1）A(4，0)，B(﹣1，0)；（2）；（3）存在，或M(0，4)或M(8，﹣4)
