题目内容
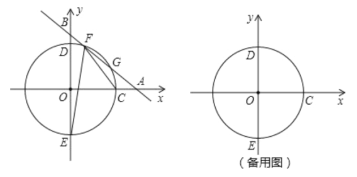
【题目】如图,AB 为圆O的直径, PQ切圆O于T , AC⊥PQ于C ,交圆O于 D .
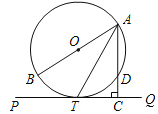
(1)求证: AT 平分∠BAC ;
(2)若 AD =2 , TC=![]() ,求圆O的半径.
,求圆O的半径.
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)PQ切⊙O于T,则OT⊥PC,根据AC⊥PQ,则AC∥OT,要证明AT平分∠BAC,只要证明∠TAC=∠ATO就可以了.
(2)过点O作OM⊥AC于M,则满足垂径定理,在直角△AOM中根据勾股定理就可以求出半径OA.
试题解析:(1)连接OT;
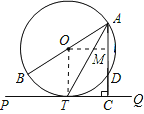
∵PQ切⊙O于T,
∴OT⊥PQ,
又∵AC⊥PQ,
∴OT∥AC,
∴∠TAC=∠ATO;
又∵OT=OA,
∴∠ATO=∠OAT,
∴∠OAT=∠TAC,
即AT平分∠BAC.
(2)过点O作OM⊥AC于M,
∴AM=MD=![]() =1;
=1;
又∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM为矩形,
∴OM=TC=![]() ,
,
∴在Rt△AOM中,
AO=![]() =
=![]() =2;
=2;
即⊙O的半径为2.

练习册系列答案
相关题目
【题目】书籍是人类进步的阶梯,联合国教科文组织把每年的4月23日确定为“世界读书日”,某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数 | 43 | 31 | 15 | 5 | 4 | 2 |
请你根据以上信息解答下列问题:
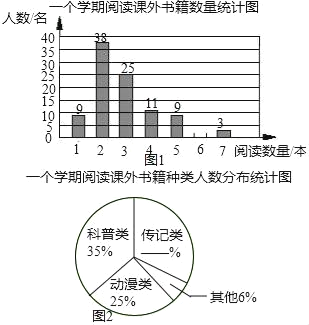
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有1200名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.