题目内容
【题目】在正方形![]() 中,点
中,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() .
.
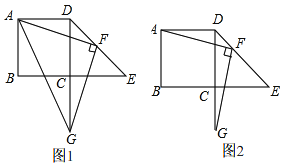
(1)如图1,填空:![]() _____________;
_____________;
(2)如图1,连接![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,若![]() 时,求证:DG=
时,求证:DG=![]() +AD.
+AD.
【答案】(1)135°;(2)20;(3)见解析
【解析】
(1)根据题意得出∠ADC=90°,∠CDE=45°,即可得出结果;
(2)先判断出∠ADF=∠GCF,进而得出△ADF≌△GCF,可得△AFG是等腰直角三角形,过F作FH⊥AD,交AD延长线于H,利用勾股定理和等腰三角形的性质求出AF和FG,即可得到△AFG的面积;
(3)过点F作FM⊥DE,证明△ADF≌△GMF,得出AD=MG,最后用等量代换即可得到结果.
解:(1)∵四边形ABCD为正方形,
∴∠ADC=∠DCB=∠DCE=90°,
∵CE=CD,
∴∠CDE=∠CED=45°,
∴∠ADE=90°+45°=135°;
(2)如图1,连接CF,
在Rt△CDE中,CE=CD,DF=EF,
∴CF=DF=EF,∠ECF=∠CDE=45°,
∴∠FCG=∠GCE+∠ECF=135°,
∴∠ADF=∠GCF=135°,
∵AF⊥FG,CF⊥DE,
∴∠AFG=∠DFC=90°,
∴∠AFD=∠GFC,
在△ADF和△GCF中,
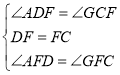 ,
,
∴△ADF≌△GCF(ASA),
∴AF=FG,
∵∠AFG=90°,
∴△AFG是等腰直角三角形,
过F作FH⊥AD,交AD延长线于H,
可知∠FDH=45°,即△FDH为等腰直角三角形,
设HF=DH=x,
∵AD=4=CD,
∴DE=![]() ,
,
∴DF=![]() ,
,
∴![]() ,
,
解得x=2,即DH=HF=2,AH=6,
∴在△AFH中,
AF=![]() =FG,
=FG,
∴S△AFG=![]() =20;
=20;
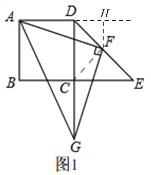
(3)如图2,过点F作FM⊥DE,
由(1)知,∠CDE=45°,
∴△DFM为等腰直角三角形,
∴DM=![]() DF,DF=MF,∠DMF=45°,
DF,DF=MF,∠DMF=45°,
∴∠GMF=135°=∠ADF,
∵MF⊥DE,
∴∠DFM=90°,
又∵∠AFG=90°,
∴∠AFD=∠GFM,
在△ADF和△GMF中,
 ,
,
∴△ADF≌△GMF(ASA),
∴AD=MG,
∴DG=DM+MG=![]() DF+AD.
DF+AD.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 | | 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 | | ( |
A.5
B.6
C.7
D.8



