Question

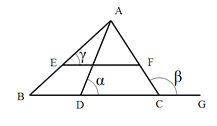
【题目】已知等边△ABC中，点D，E分别在边AB， BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′，EB′分别交边AC于点F，G，若∠ADF=80°，则∠EGC的度数为（ ）。

A. 70°B. 75°C. 80°D. 85°

Answer 1

【答案】C

【解析】

根据△DEB′是△BDE沿直线DE翻折得到的，得到∠B=∠B′，根据等边三角形的性质可得∠A=∠C=∠B=60°，根据三角形内角和定理可求得∠AFD=40°，继而可求得∠∠B′GF=80°，再根据对顶角的性质即可求得答案.

∵△DEB′是△BDE沿直线DE翻折得到的，

∴∠B=∠B′，

∵△ABC是等边三角形，

∴∠A=∠C=∠B=60°，

∵∠A+∠ADF+∠AFD=180°，∠ADF=80°，

∴∠AFD=180°-60°-80°=40°，

∵∠B′FG+∠B′GF+∠B′=180°，∠B′FG=∠AFD，

∴∠B′GF=180°-60°-40°=80°，

∴∠EGC=∠B′GF=80°，

故选C．