Question

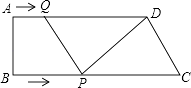
【题目】如图，在△ABC中，AB=AC，AD平分∠BAC交BC于点D，分别过点A，D作AE∥BC，DE∥AB，AE与DE相交于点E，连结CE．
（1）求证：AE=BD；
（2）求证：四边形ADCE是矩形．

Answer 1

【答案】
（1）证明：∵AE∥BC、DE∥AB，

∴四边形ABDE是平行四边形．

∴AE=BD

（2）证明：由（1）得：AE=BD，

∵AB=AC，AD平分∠BAC，

∴BD=CD，AD⊥BC，

∴AE=CD，∠ADC=90°，

又∵AE∥BC，

∴四边形ADCE是平行四边形．

∴四边形ADCE是矩形

【解析】（1）先证明四边形ABDE是平行四边形，得出AE=BD即可；（2）由等腰三角形的性质得出BD=CD，AD⊥BC，得出AE=CD，∠ADC=90°，证出四边形ADCE是平行四边形．即可得出结论．
【考点精析】本题主要考查了平行线的性质和等腰三角形的性质的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；等腰三角形的两个底角相等（简称：等边对等角）才能正确解答此题．