题目内容
【题目】如图，四边形ABCD中，∠BAD＝∠C＝90°，AB＝AD，AE⊥BC，垂足为E．若线段AE＝2，则四边形ABCD的面积是_____．
【答案】4
【解析】
过点A作AF⊥AE，交CD的延长线于点F，由题意可证△ABE≌△ADF，可得AE＝AF，则可证四边形AECF是正方形，四边形ABCD的面积＝正方形AECF的面积＝4．
解：过点A作AF⊥AE，交CD的延长线于点F
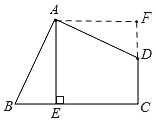
∵∠BAD＝∠C＝90°，AE⊥BC，AE⊥AF
∴四边形AECF是矩形
∴∠F＝90°
∵AE⊥AF，BA⊥AD
∴∠BAE+∠DAE＝90°，∠DAF+∠DAE＝90°
∴∠BAE＝∠DAF
又∵AB＝AD，∠F＝∠AEB＝90°
∴△ADF≌△ABE
∴AF＝AE，S△ADF＝S△ABE．
∴四边形AECF是正方形．
∴S正方形AECF＝
＝4
∵S四边形ABCD＝S△ABE+S四边形AECD＝S△ADF+S四边形AECD．
∴S四边形ABCD＝S正方形AECF＝4
故答案为：4
练习册系列答案
名校课堂系列答案
相关题目
