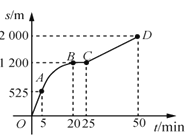
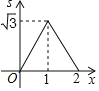题目内容
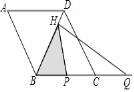
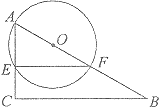
【题目】如图,五边形![]() 内接于
内接于![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
(1)若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由圆心角、弧、弦之间的关系得出![]() ,由圆周角定理得出∠ADE=∠DBC,证明△ADE≌△DBC,即可得出结论;
,由圆周角定理得出∠ADE=∠DBC,证明△ADE≌△DBC,即可得出结论;
(2)连接CO并延长交AB于G,作OH⊥AB于H,则∠OHG=∠OHB=90°,由切线的性质得出∠FCG=90°,得出△CFG、△OGH是等腰直角三角形,得出CF=CG,OG=![]() OH,由等边三角形的性质得出∠OBH=30°,由直角三角形的性质得出OH=
OH,由等边三角形的性质得出∠OBH=30°,由直角三角形的性质得出OH=![]() OB=1,OG=
OB=1,OG=![]() ,即可得出答案.
,即可得出答案.
(1)证明:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,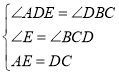 ,
,
∴![]() ,
,
∴![]() ;
;
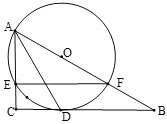
(2)解:连接![]() 并延长交
并延长交![]() 于
于![]() ,作
,作![]() 于
于![]() ,如图所示:
,如图所示:
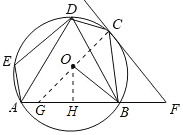
则![]() ,
,
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 、
、![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目