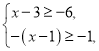题目内容
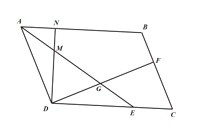
【题目】如图,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 经过点
经过点![]() ,与
,与![]() 相交于点E,与
相交于点E,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
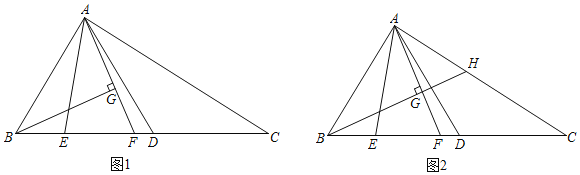
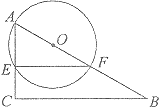
(I).如图,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
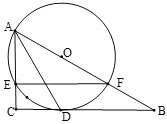
(II)如图,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() .
.
①求证:![]() 为
为![]() 的切线;
的切线;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)AF=4;(Ⅱ)①证明见解析;②AF=5.
【解析】
(Ⅰ)由AF为⊙O的直径可得∠AEF=90°,根据三角形内角和可求出∠BAC=60°,即可求出∠AFE=30°,根据含30°角的直角三角形的性质求出AF的长即可;(Ⅱ)①连接OD,根据角平分线的定义可得![]() ,由等腰三角形的性质可得
,由等腰三角形的性质可得![]() ,即可证明OD//AC,根据平行线的性质即可得结论;②设OD与EF交于点H,可证明四边形CDHE是矩形,可得EH=CD=2,根据垂径定理可求出EF的长,利用勾股定理求出AF的长即可.
,即可证明OD//AC,根据平行线的性质即可得结论;②设OD与EF交于点H,可证明四边形CDHE是矩形,可得EH=CD=2,根据垂径定理可求出EF的长,利用勾股定理求出AF的长即可.
(Ⅰ)∵AF为⊙O的直径,
![]()
![]() .
.
∵![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() AF=2AE=4.
AF=2AE=4.
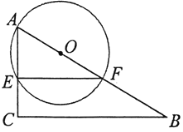
(Ⅱ)①连接OD.
∵DA平分![]() ,
,
![]() ,
,
∵OA=OD,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
∵∠C=90°,
![]()
![]() ,
,
即![]() ,
,
![]() BC为⊙O的切线.
BC为⊙O的切线.

②设OD与EF交于点H,
∵![]() ,
,
![]() 四边形CDHE为矩形.
四边形CDHE为矩形.
![]() EH=CD=2,
EH=CD=2,![]() .
.
![]()
![]() .
.
![]() EF=2EH=4.
EF=2EH=4.
![]()
![]() .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.