题目内容
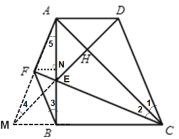
【题目】在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF∥CD,AF⊥CE的延长线于F.连接DE交对角线AC于H.下列结论:①AC垂直平分ED;②AE=BE;③CE=2BF;④BE=2EF.其中结论正确的是_______.(填序号)

【答案】①③
【解析】
根据△ABC是等腰直角三角形,得出∠BAC=∠BCA=45°,再由AD∥BC得出AC平分∠EAD,又因为AE=AD所以AC是DE的垂直平分线即AC垂直平分ED;延长AF和CB交于点M,连接EM,F、A、B、C四点共圆,F、E、B、M四点共圆,AE=ME>BE;由△AMB≌△CEB, 得出BF=![]() AM,即CE=2BF;作FN∥MB,推出BE<2EF.
AM,即CE=2BF;作FN∥MB,推出BE<2EF.
解:∵∠ABC=90°,AB=BC
∴△ABC是等腰直角三角形
∴∠BAC=∠BCA=45°
∵AD∥BC,
∴∠CAD=∠BCA
∴∠BAC=∠CAD
∴AC平分∠EAD
∵AE=AD
∴AC垂直平分ED①正确;
延长AF和CB交于点M,连接EM,M、E、D在一条直线上,
由F、A、B、C四点共圆,F、E、B、M四点共圆,
可得∠1=∠2=∠3=∠4,∠FBM=45°+∠1, ∠FMB=45°+∠4,
∴FM=FM,FA=FB, ∠5=∠3=∠4,AE=ME>BE故②不成立;由△AMB≌△CEB,可得CE=AM,F是MA的中点,BF=![]() AM, ∴CE=2BF,故③成立;作FN∥MB,可得BE=BM=2FN,故FN<EF,故BE<2EF,④不成立;故答案为:①③.
AM, ∴CE=2BF,故③成立;作FN∥MB,可得BE=BM=2FN,故FN<EF,故BE<2EF,④不成立;故答案为:①③.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目