题目内容
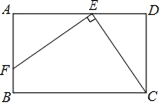
【题目】(1)如图所示,BD,CE是![]() 的高,点P在BD的延长线上,
的高,点P在BD的延长线上,![]() ,点Q在CE上,
,点Q在CE上,![]() ,探究PA与AQ之间的关系;
,探究PA与AQ之间的关系;
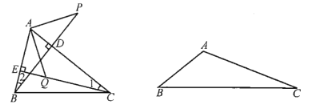
(2)若把(1)中的![]() 改为钝角三角形,
改为钝角三角形,![]() ,
,![]() 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
【答案】(1)![]() ,
,![]() ;(2)成立,证明见解析.
;(2)成立,证明见解析.
【解析】
(1)根据同角的余角相等可得![]() ,然后利用SAS即可证出
,然后利用SAS即可证出![]() ,从而得出
,从而得出![]() ,
,![]() ,然后根据直角三角形的性质和等量代换即可求出
,然后根据直角三角形的性质和等量代换即可求出![]() ,从而得出结论;
,从而得出结论;
(2)先根据题意,补全图形,如解图所示,根据等角的余角相等可得![]() ,然后利用SAS即可证出
,然后利用SAS即可证出![]() ,从而得出
,从而得出![]() ,
,![]() ,然后根据直角三角形的性质和等量代换即可求出
,然后根据直角三角形的性质和等量代换即可求出![]() ,从而得出结论.
,从而得出结论.
解:(1)∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]()
∴![]()
即![]() .
.
∴![]() .
.
即![]() ,
,![]() .
.
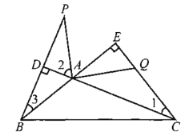
(2)上述结论仍然成立.如图所示
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
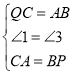
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() ,
,
即![]() ,
,![]() .
.

练习册系列答案
相关题目