题目内容
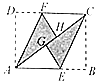
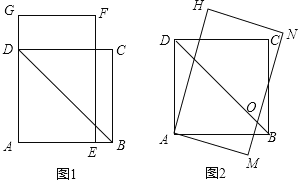
【题目】如图1,四边形ABCD是边长为![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
(1)求∠DOM的度数;
(2)图2中,求D、N两点间的距离;
(3)若将矩形AMNH绕点A再顺时针旋转15°得到矩形APQR,此时点B在矩形APQR的内部、外部还是边上?并说明理由.
【答案】(1)120°;(2)![]() ;(3)点B在矩形APQR的内部.
;(3)点B在矩形APQR的内部.
【解析】试题分析:(1)由旋转的性质,可得∠BAM=15°,即可得∠OKB=∠AOM=75°,又由正方形的性质,可得∠ABD=45°,然后利用外角的性质,即可求得∠DOM的度数;
(2)首先连接AM,交BD于I,连接AN,由特殊角的三角函数值,求得∠HAN=30°,又由旋转的性质,即可求得∠DAN=45°,即可证得A,C,N共线,然后由股定理求得答案;
(3)在Rt△ARK中,利用三角函数即可求得AK的值,与AB比较大小,即可确定B的位置.
试题解析:(1)依题意得:∠BAM=15°,
设MN与AB交于K,
∵四边形AMNH是矩形,
∴∠M=90°,
∴∠AKM=90°-∠BAM=75°.
∴∠BKO=∠AKM=75°.
∵四边形ABCD是正方形,
∴∠ABD=45°.
∴∠DOM=∠BKO+∠ABD=75°+45°=120°.
(2)连接AN,交BD于I,连接DN
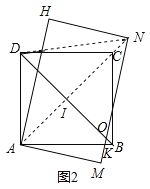
∵AE=4,∠AFE=30°,∠AEF=90°,
∴AN=AF=2AE=8.
由旋转得:∠DAH=15°,
∴∠DAN=45°.
∵正方形ABCD中,∠DAC=45°.
∴A、C、N共线.
∵正方形ABCD中,BD⊥AC,AD=AB=![]() ,
,
∴DI=AI=![]() .
.
∴NI=AN-AI=8-3=5.
∴Rt△DIN中, ![]() .
.
(3)点B在矩形APQR的内部,理由如下:
如图,
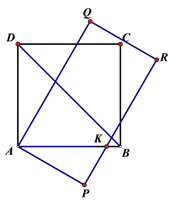
依题意得:∠BAP=15°+15°=30°,
∵∠P=90°,
∴AK=2PK.
∵AP=4,AP2+PK2=AK2,
解得: ![]() ,
,
∵AB=![]() ,
,
∴点B在矩形APQR的内部.

 发散思维新课堂系列答案
发散思维新课堂系列答案