题目内容
【题目】现有七个数﹣1，﹣2，﹣2，﹣4，﹣4，﹣8，﹣8将它们填入图1（3个圆两两相交分成7个部分）中，使得每个圆内部的4个数之积相等，设这个积为m，如图2给出了一种填法，此时m＝64，在所有的填法中，m的最大值为_____．
【答案】128
【解析】
观察图象，可得这7个数，有的被乘了1次，2次，3次．要使得每个圆内部的4个数之积相等且最大所以﹣8，﹣8必须放在被乘两次的位置．与﹣8，﹣8同圆的只能为﹣1，﹣2，其中﹣2放在中心位置，可得m＝128.
解：观察图象，可得这7个数，有的被乘了1次，2次，3次．要使得每个圆内部的4个数之积相等且最大所以﹣8，﹣8必须放在被乘两次的位置．与﹣8，﹣8同圆的只能为﹣1，﹣2，其中﹣2放在中心位置，如图
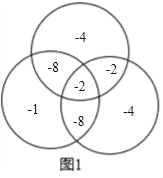
∴m＝（﹣8）×（﹣8）×（﹣1）×（﹣2）＝128．
故答案为：128．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】观察下面三行数：
第1列 | 第2列 | 第3列 | 第4列 | … | 第n列 |
﹣3 | 9 | a | 81 | … | r |
1 | ﹣3 | 9 | b | … | s |
﹣2 | 10 | c | 82 | … | t |
（1）直接写出a，b，c的值；
（2）直接写出r，s，t的值；
（3）设x，y，z分别为第①②③行的第2019个数，求x+6y+z的值．
