题目内容
【题目】观察下面三行数:
第1列 | 第2列 | 第3列 | 第4列 | … | 第n列 |
﹣3 | 9 | a | 81 | … | r |
1 | ﹣3 | 9 | b | … | s |
﹣2 | 10 | c | 82 | … | t |
(1)直接写出a,b,c的值;
(2)直接写出r,s,t的值;
(3)设x,y,z分别为第①②③行的第2019个数,求x+6y+z的值.
【答案】(1)a=﹣27,b=﹣27,c=﹣26;(2)r=(﹣1)n×3n,![]() ,t=(﹣1)n×3n+1;(3)x+6y+z=1.
,t=(﹣1)n×3n+1;(3)x+6y+z=1.
【解析】
(1)根据表格中的数据可以写出每列中第n个数的式子,从而可以求得a,b,c的值;
(2)根据表格中的数据可以写出每列中第n个数的式子,从而可以得到r,s,t的值;
(3)根据(2)中的结果可以得到x,y,z的值,从而可以求得所求式子的值.
解:(1)由表可得,
第一行第n个数是:(﹣1)n×3n,
第二行第n个数是:![]() ,
,
第三行第n个数是:(﹣1)n×3n+1,
∴a=(﹣1)3×33=﹣27,
b=![]() =﹣27,
=﹣27,
c=(﹣1)3×33+1=﹣26,
即a=﹣27,b=﹣27,c=﹣26;
(2)由表可得,
第一行第n个数是:(﹣1)n×3n,
第二行第n个数是:![]() ,
,
第三行第n个数是:(﹣1)n×3n+1,
则r=(﹣1)n×3n,s=![]() ,t=(﹣1)n×3n+1;
,t=(﹣1)n×3n+1;
(3)当n=2019时,
x=(﹣1)2019×32019=﹣32019,
y=![]() =32018,
=32018,
z=(﹣1)2019×32019+1=﹣32019+1,
∴x+6y+z
=﹣32019+6×32018+(﹣32019+1)
=﹣32019+2×32019﹣32019+1
=1.
故答案为:(1)a=﹣27,b=﹣27,c=﹣26;(2)r=(﹣1)n×3n,s=![]() ,t=(﹣1)n×3n+1;(3)x+6y+z=1.
,t=(﹣1)n×3n+1;(3)x+6y+z=1.

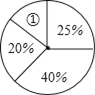
【题目】物理兴趣小组20位同学在实验操作中的得分情况如下表:(Ⅰ)求这组数据的众数、中位数;(Ⅱ)求这组数据的平均数;(Ⅲ)将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
得分(分) | 10 | 9 | 8 | 7 |
人数(人) | 5 | 8 | 4 | 3 |
【题目】某学习小组在研究函数y= ![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
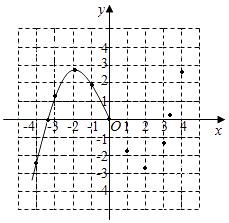
(1)请补全函数图象;
(2)方程 ![]() x3﹣2x=﹣2实数根的个数为;
x3﹣2x=﹣2实数根的个数为;
(3)观察图象,写出该函数的两条性质.