题目内容
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AB=AD,
∵DF⊥AG,BE⊥AG,
∴∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中,
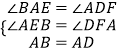 ,
,
∴△ABE≌△DAF(AAS).
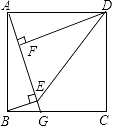
(2)设EF=x,则AE=DF=x+1,
由题意2× ![]() ×(x+1)×1+
×(x+1)×1+ ![]() ×x×(x+1)=6,
×x×(x+1)=6,
解得x=2或﹣5(舍弃),
∴EF=2.
【解析】(1)运用正方形的性质,利用角角边很容易判定全等;(2)根据ABED的面积为6,可表示为三个三角形面积之和,用EF的代数式表示面积,构建方程即可.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目