ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦ1Θ§…δœΏOPΓΈAEΘ§ΓœAOPΒΡΫ«ΤΫΖ÷œΏΫΜ…δœΏAE”ΎΒψBΘ°
Θ®1Θ©»τΓœA=50ΓψΘ§«σΓœABOΒΡΕ» ΐΘΜ
Θ®2Θ©»γΆΦ2Θ§»τΒψC‘Ύ…δœΏAE…œΘ§OBΤΫΖ÷ΓœAOCΫΜAE”ΎΒψBΘ§ODΤΫΖ÷ΓœCOPΫΜAE”ΎΒψDΘ§ΓœABO-ΓœAOB=70ΓψΘ§«σΓœADOΒΡΕ» ΐΘΜ
Θ®3Θ©»γΆΦ3Θ§»τΓœA=ΠΝΘ§“ά¥ΈΉς≥ωΓœAOPΒΡΫ«ΤΫΖ÷œΏOBΘ§ΓœBOPΒΡΫ«ΤΫΖ÷œΏOB1Θ§ΓœB1OPΒΡΫ«ΤΫΖ÷œΏOB2Θ§Γ≠Θ§ΓœBn-1OPΒΡΫ«ΤΫΖ÷œΏOBnΘ§Τδ÷–ΒψBΘ§B1Θ§B2Θ§Γ≠Θ§Bn-1Θ§BnΕΦ‘Ύ…δœΏAE…œΘ§ ‘«σΓœABnOΒΡΕ» ΐΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©65ΓψΘΜΘ®2Θ©35ΓψΘΜΘ®3Θ©ΓœABnO=![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟ≥ωΓœA=Γœ1=50ΓψΘ§ΗυΨίΤΫΫ«ΒΡΕ®“ε«σΒΟΓœAOP=130ΓψΘ§ΗυΨίΫ«ΤΫΖ÷œΏΒΡ–‘÷ ΚΆΤΫ––œΏΒΡ–‘÷ «σΒΟΓœABO=Γœ2=65ΓψΘΜ
Θ®2Θ©“ρΈΣΓœABO=ΓœACO+ΓœBOCΘ§ΓœABO-ΓœAOB=70ΓψΘ§ΓœBOC=ΓœAOBΘ§«σΒΟΓœACO=70ΓψΘ§ΗυΨίΤΫ––œΏΒΡ–‘÷ «σΒΟΓœCOP=ΓœACO=70ΓψΘ§ΫχΕχΦ¥Ω…«σΒΟΓœADO=35ΓψΘ°
Θ®3Θ©ΗυΨίΘ®1Θ©Θ®2Θ©ΒΡΙφ¬…Φ¥Ω…«σΒΟΘ°
Θ®1Θ©»γΆΦ1Θ§
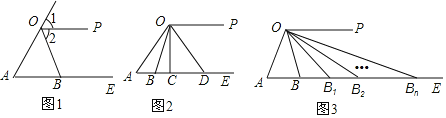
ÿOPøAEȧ
ΓύΓœA=Γœ1=50ΓψΘ§
ΓύΓœAOP=130ΓψΘ§
ΓΏΓœ2=ΓœAOBΘ§
ΓύΓœ2=65ΓψΘ§
ΓύΓœABO=Γœ2=65ΓψΘΜ
Θ®2Θ©»γΆΦ2Θ§ΓΏΓœABO=ΓœACO+ΓœBOCΘ§ΓœABO-ΓœAOB=70Γψ
ΓύΓœACO+ΓœBOC-ΓœAOB=70ΓψΘ§
ΓΏΓœBOC=ΓœAOBΘ§
ΓύΓœACO=70ΓψΘ§
ÿOPøAEȧ
ΓύΓœCOP=ΓœACO=70ΓψΘ§ΓœPOD=ΓœADOΘ§
ΓΏΓœPOD=ΓœCOD=![]() ΓœCOP=35Γψ
ΓœCOP=35Γψ
ΓύΓœADO=35ΓψΘ°
Θ®3Θ©»γΆΦ3Θ§”…Θ®1Θ©Ω…÷ΣΘ§ΓœABO=![]() Θ®180Γψ-ΠΝΘ©Θ§ΓœAB1O=
Θ®180Γψ-ΠΝΘ©Θ§ΓœAB1O=![]() Θ®180Γψ-ΓœOBB1Θ©=
Θ®180Γψ-ΓœOBB1Θ©=![]() ΓœABO=
ΓœABO=![]() Θ®180Γψ-ΠΝΘ©Θ§ΓœAB2O=
Θ®180Γψ-ΠΝΘ©Θ§ΓœAB2O=![]() Θ®180Γψ-ΠΝΘ©Θ§Γ≠
Θ®180Γψ-ΠΝΘ©Θ§Γ≠
‘ρΓœABnO=![]() Θ°
Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
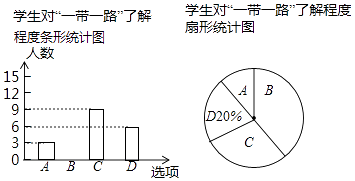
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΈοάμ–Υ»Λ–ΓΉι20ΈΜΆ§―ß‘Ύ Β―ι≤ΌΉς÷–ΒΡΒΟΖ÷«ιΩω»γœ¬±μΘΚΘ®ΔώΘ©«σ’βΉι ΐΨίΒΡ÷Ύ ΐΓΔ÷–ΈΜ ΐΘΜΘ®ΔρΘ©«σ’βΉι ΐΨίΒΡΤΫΨυ ΐΘΜΘ®ΔσΘ©ΫΪ¥Υ¥Έ≤ΌΉςΒΟΖ÷Α¥»Υ ΐ÷Τ≥…»γΆΦΥυ ΨΒΡ…»–ΈΆ≥ΦΤΆΦΘ°…»–ΈΔΌΒΡ‘≤–ΡΫ«Ε» ΐ «Εύ…ΌΘΩ
ΒΟΖ÷Θ®Ζ÷Θ© | 10 | 9 | 8 | 7 |
»Υ ΐΘ®»ΥΘ© | 5 | 8 | 4 | 3 |
ΓΨΧβΡΩΓΩΡ≥―ßœΑ–ΓΉι‘Ύ―–ΨΩΚ· ΐy= ![]() x3©¹2xΒΡΆΦœσ”κ–‘÷ ±Θ§“―Ν–±μΓΔΟηΒψ≤ΔΜ≠≥ωΝΥΆΦœσΒΡ“Μ≤ΩΖ÷Θ°
x3©¹2xΒΡΆΦœσ”κ–‘÷ ±Θ§“―Ν–±μΓΔΟηΒψ≤ΔΜ≠≥ωΝΥΆΦœσΒΡ“Μ≤ΩΖ÷Θ°
x | Γ≠ | ©¹4 | ©¹3.5 | ©¹3 | ©¹2 | ©¹1 | 0 | 1 | 2 | 3 | 3.5 | 4 | Γ≠ |
y | Γ≠ | ©¹ | ©¹ |
|
|
| 0 | ©¹ | ©¹ | ©¹ |
|
| Γ≠ |
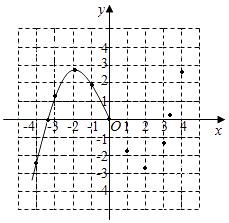
Θ®1Θ©«κ≤Ι»ΪΚ· ΐΆΦœσΘΜ
Θ®2Θ©ΖΫ≥Χ ![]() x3©¹2x=©¹2 Β ΐΗυΒΡΗω ΐΈΣΘΜ
x3©¹2x=©¹2 Β ΐΗυΒΡΗω ΐΈΣΘΜ
Θ®3Θ©Ιέ≤λΆΦœσΘ§–¥≥ωΗΟΚ· ΐΒΡΝΫΧθ–‘÷ Θ°