题目内容
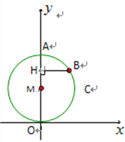
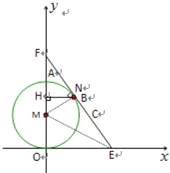
【题目】如图8,在平面直角坐标系中,点A坐标为(0,3),点B(![]() ,
,![]() )是以OA为直径的⊙M上的一点,且tan∠AOB=
)是以OA为直径的⊙M上的一点,且tan∠AOB=![]() ,BH⊥
,BH⊥![]() 轴,H为垂足,点C(
轴,H为垂足,点C(![]() ,
,![]() ).
).
(1)求H点的坐标;
(2)求直线BC的解析式;
(3)直线BC是否与⊙M相切?请说明理由.
【答案】(1) H(0,![]() ); (2)
); (2) ![]() =-
=-![]()
![]() +4;(3)见解析.
+4;(3)见解析.
【解析】分析:
(1)由已知易得tan∠AOB=![]() ,BH=
,BH=![]() ,由此即可解得m=
,由此即可解得m=![]() ,从而可得点H的坐标;
,从而可得点H的坐标;
(2)由(1)可知点B的坐标为![]() 结合点C的坐标即可由待定系数法求得直线BC的解析式;
结合点C的坐标即可由待定系数法求得直线BC的解析式;
(3)设直线BC与两坐标轴的交点分别为E、F,由(2)中所得解析式可求得点E、F的坐标,过点M作MN⊥BC于点N,由S△FME=![]() EF·MN=
EF·MN=![]() FM·EO,可证得MN的长等于⊙M的半径,由此即可得到BC是⊙M的切线.
FM·EO,可证得MN的长等于⊙M的半径,由此即可得到BC是⊙M的切线.
详解:
(1)由tan∠AOB=![]() ,得
,得![]() =
=![]() ,
,
∴OH=2BH,又B(![]() ,
,![]() ),即
),即![]() =2×
=2×![]() =
=![]() ,
,
∴H点的坐标为H(0,![]() );
);
(2)设过点B(![]() ,
,![]() )及点C(
)及点C(![]() ,
,![]() )
)
的直线解析式为:![]() =
=![]() +
+![]() ,
,
把BC坐标分别代入,得: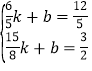 ,
,
解得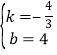 ,
,
∴直线BC的解析式为:![]() =-
=-![]()
![]() +4;
+4;
(3)BC与⊙M相切,理由如下
如下图,设直线BC:![]() 分别与
分别与![]() 轴
轴![]() 轴交于点EF,
轴交于点EF,
则点E的坐标为(3,0)点F的坐标为(0,4),
∴OE=3,OF=4,
∴EF=5,
过圆心M作MN⊥EF,垂足为N,连结ME,
∵S△FME=![]() EF·MN=
EF·MN=![]() FM·EO,
FM·EO,
∴得EF·MN=FM·EO,
∵⊙M的直径为3,
∴⊙M的半径OM=1.5,
∴MF=4-1.5=2.5,
∴MN=![]() =
=![]() ,
,
即圆心M到直线BC的距离等于⊙M的半径,
∴直线BC是⊙M的切线.

练习册系列答案
相关题目