题目内容
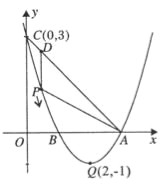
【题目】如图,已知抛物线![]() 的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
【1】求该抛物线的函数关系式;
【1】求点P在运动的过程中,线段PD的最大值;
【1】当△ADP是直角三角形时,求点P的坐标;
【1】在题(3)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
【答案】
【1】![]()
【1】设点P (x, ![]() ) 直线PD的解析式为
) 直线PD的解析式为![]()
设PD=m, 则m=![]() (
(![]() )=
)=![]() =
=![]()
PD的最大值![]() .
.
【1】P (1,0) 或(2,-1)
【1】当P (1,0),A、B、E三点共线,所以此种情况不存在。
当P(2,-1)时,F(![]() 或
或![]()
【解析】
【1】主要考查了抛物线解析式的求解
【1】运用两点的距离公式得到PD=m, 则m=![]() (
(![]() )=
)=![]() =
=![]()
PD的最大值![]()
【1】利用△ADP是直角三角形时垂直关系得到结论。
【1】在第三问的基础上,利用假设存在以A、P、E、F为顶点的平行四边形得到。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
a | a+2 | a+4 | … |
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?