题目内容
【题目】阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;

我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
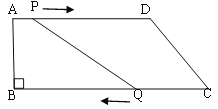
如图,我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
⑴写出筝形的两个性质(定义除外);
⑵写出筝形的两个判定方法(定义除外),并选出一个进行证明.

【答案】解:(1)
性质1:只有一组对角相等(或者∠B=∠D,∠A≠∠C); …………………………1分
性质2:只有一条对角线平分对角; ……………………………………………………2分
性质有如下参考选项:
性质3:两条对角线互相垂直,其中只有一条被另一条平分;
性质4:两组对边都不平行.
(2)判定方法1:只有一条对角线平分对角的四边形是筝形;…………………………4分
判定方法2:两条对角线互相垂直且只有一条被平分的四边形是筝形;…………………6分
判定方法有如下参考选项:
判定方法3:AC⊥BD,∠B=∠D,∠A≠∠C;
判定方法4:AB=CD,∠B=∠D,∠A≠∠C;
判定方法5:AC⊥BD, AB=CD,∠A≠∠C.
判定方法1的证明:
已知:在四边形ABCD中,对角线AC平分∠A和∠C,对角线BD不平分∠B和∠D.
求证:四边形ABCD是筝形.
证明:∵∠BAC=∠DAC,∠BCA=∠DCA,AC=AC,∴△ABC≌△ADC.
∴AB=CD,CB=CD,①…………………………………………………………………8分
易知AC⊥BD.
又∵∠ABD≠∠CBD,
∴∠BAC≠∠BCA,∴AB≠BC.②……………………………………………………10分
由①、②知四边形ABCD是筝形.……………………………………………………11分
判定方法2的证明:
AC⊥BD,(不妨)BE=DE→AB=CD,CB=CD.AE≠CE→AB≠BC.
判定方法3的证明:
若B、D不是关于AC对称,则有∠ABD<∠ADB,∠CBD<∠CDB(或反之)→与∠B=∠D矛盾→B、D关于AC对称→AB=CD,CB=CD. ∠A≠∠CAE→∠BAC≠∠BCA→AB≠BC.
判定方法4的证明:
AB=CD→∠ABD=∠ADB(结合∠B=∠D)→∠CBD=∠CDB →CB=CD.
以下同判定方法3.
判定方法5的证明:对照3和4 的证明.
其他判定方法及证明参照给分.
【解析】略

 期末集结号系列答案
期末集结号系列答案【题目】某日孙老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5.
项目 | 第一次锻炼 | 第二次锻炼 | ||
步数(步) | 10000 | ① | ||
平均步长(米/步) | 0.6 | ② | ||
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)求孙老师第二次锻炼时平均步长减少的百分率;
(2)孙老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求孙老师这500米的平均步长.
【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?