题目内容
【题目】如图1，已知O是坐标原点，点A的坐标是（5，0），点B是y轴正半轴上一动点，以OB，OA为边作矩形OBCA，点E，H分别在边BC和边OA上，将△BOE沿着OE对折，使点B落在OC上的F点处，将△ACH沿着CH对折，是点A落在OC上的G点处。
（1）求证：四边形OECH是平行四边形；
（2）如图2，当点B运动到使得点F，G重合时，判断四边形OECH的形状并说明理由；
（3）当点B运动到使得点F，G将对角线OC三等分时，求点B的坐标。
【答案】（1）证明见解析；（2）点B的坐标是（0， 
）；四边形OECH是菱形．理由见解析；（3）（0， 
）或（0，2
）．
【解析】试题分析：（1）如图1，根据矩形的性质得OB∥CA，BC∥OA，再利用平行线的性质得∠BOC=∠OCA，然后根据折叠的性质得到∠BOC=2∠EOC，∠OCA=2∠OCH，所以∠EOC=∠OCH，根据平行线的判定定理得OE∥CH，加上BC∥OA，于是可根据平行四边形的判定方法得四边形OECH是平行四边形；
（2）如图2，先根据折叠的性质得∠EFO=∠EBO=90°，∠CFH=∠CAF=90°，由点F，G重合得到EH⊥OC，根据菱形的判定方法得到平行四边形OECH是菱形，则EO=EC，所以∠EOC=∠ECO，而∠EOC=∠BOE，根据三角形内角和定理可计算出∠EOB=∠EOC=∠ECO=30°，在Rt△OBC中，根据含30度的直角三角形三边的关系得OB=
BC=
，于是得到点B的坐标是（0， 
）；
（3）分类讨论：当点F在点O，G之间时，如图3，根据折叠的性质得OF=OB，CG=CA，则OF=CG，所以AC=OF=FG=GC，设AC=m，则OC=3m，在Rt△OAC中，根据勾股定理得m2+52=（3m）2，解得m=
，则点B的坐标是（0， 
）；当点G在O，F之间时，如图4，同理可得OF=CG=AC，设OG=n，则AC=GC=2n，在Rt△OAC中，根据勾股定理得（2n）2+52=（3n）2，解得n=
，则AC=OB=2
，所以点B的坐标是（0，2
）．
试题解析：（1）证明：如图1，
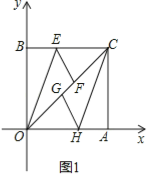
∵四边形OBCA为矩形，
∴OB∥CA，BC∥OA，
∴∠BOC=∠OCA，
又∵△BOE沿着OE对折，使点B落在OC上的F点处；△ACH沿着CH对折，使点A落在OC上的G点处，
∴∠BOC=2∠EOC，∠OCA=2∠OCH，
∴∠EOC=∠OCH，
∴OE∥CH，
又∵BC∥OA，
∴四边形OECH是平行四边形；
（2）解：点B的坐标是（0， 
）；四边形OECH是菱形．理由如下：如图2，
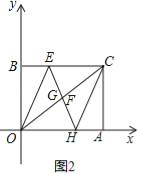
∵△BOE沿着OE对折，使点B落在OC上的F点处；△ACH沿着CH对折，使点A落在OC上的G点处，
∴∠EFO=∠EBO=90°，∠CFH=∠CAF=90°，
∵点F，G重合，
∴EH⊥OC，
又∵四边形OECH是平行四边形，
∴平行四边形OECH是菱形，
∴EO=EC，
∴∠EOC=∠ECO，
又∵∠EOC=∠BOE，
∴∠EOB=∠EOC=∠ECO=30°，
又∵点A的坐标是（5，0），
∴OA=5，
∴BC=5，
在Rt△OBC中，OB=
BC=
，
∴点B的坐标是（0， 
）；
（3）解：当点F在点O，G之间时，如图3，
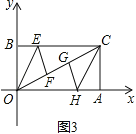
∵△BOE沿着OE对折，使点B落在OC上的F点处；△ACH沿着CH对折，使点A落在OC上的G点处，
∴OF=OB，CG=CA，
而OB=CA，
∴OF=CG，
∵点F，G将对角线OC三等分，
∴AC=OF=FG=GC，
设AC=m，则OC=3m，
在Rt△OAC中，OA=5，
∵AC2+OA2=OC2，
∴m2+52=（3m）2，解得m=
，
∴OB=AC=
，
∴点B的坐标是（0， 
）；
当点G在O，F之间时，如图4，
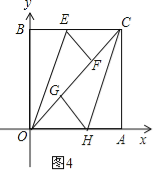
同理可得OF=CG=AC，
设OG=n，则AC=GC=2n，
在Rt△OAC中，OA=5，
∵AC2+OA2=OC2，
∴（2n）2+52=（3n）2，解得n=
，
∴AC=OB=2
，
∴点B的坐标是（0，2
）．
